


suivant: Autres applications
monter: Développement de Taylor, séries
précédent: Série alternée
Index
La fonction logarithme
Si nous voulons calculer ln(1 + x) pour
x 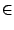 [0, 1[ avec une
précision
[0, 1[ avec une
précision
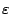 , il suffit de calculer
, il suffit de calculer
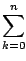
(- 1)
k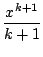
pour n tel que la valeur absolue du terme suivant soit plus petit
que
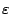 :
:
n tel que
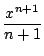
<
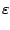
en effet, les signes sont alternés et la suite
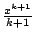 décroit vers 0.
décroit vers 0.
Si la suite décroit lentement vers 0, cette méthode est
mauvaise numériquement et en temps de calcul
car il y a presque compensation entre
termes successifs donc perte de précision sur la mantisse et il
y a beaucoup de termes à calculer. C'est le cas pour le logarithme,
si x est voisin de 1, il faut calculer n termes pour avoir une
précision en 1/n, par exemple 1 million de termes pour avoir
une précision de 1e - 6 (sans tenir compte des erreurs d'arrondi).
Si x est proche de 1/2 il faut de l'ordre
de
-ln(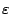 )/ln(2) termes ce qui est mieux, mais encore
relativement grand (par exemple
50 termes environ pour une précision en 1e - 16,
13 termes pour 1e - 4).
On a donc intérêt à se
ramener si possible à calculer la fonction en un x où la
convergence est plus rapide (donc | x| le plus petit possible).
Par exemple pour le calcul de ln(1 + x) on peut :
)/ln(2) termes ce qui est mieux, mais encore
relativement grand (par exemple
50 termes environ pour une précision en 1e - 16,
13 termes pour 1e - 4).
On a donc intérêt à se
ramener si possible à calculer la fonction en un x où la
convergence est plus rapide (donc | x| le plus petit possible).
Par exemple pour le calcul de ln(1 + x) on peut :
- utiliser la racine carrée
ln(1 +
x) = 2
ln(
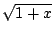
)
on observe que :
il faut toutefois faire attention à la perte de précision sur
X par rapport à x lorsque x est petit.
- utiliser l'inverse
ln(1 +
x) = - ln(1/(1 +
x)) = - ln(1 +
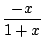
)
- trouver une valeur approchée y0 de ln(1 + x) à une précision
faible, par exemple 1e - 4, et utiliser la méthode de Newton pour
améliorer la précision. Soit en effet
y = ln(1 + x), alors
ey = 1 + x, on pose
f (y) = ey - (1 + x), on utilise la suite itérative
yn+1 =
yn -
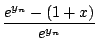
Comme y0 est proche à 1e - 4 de y, on peut espérer avoir
une valeur approchée de y à 1e - 16 en 2 itérations. Notez
que y est proche de 0, on est dans un domaine où le calcul
de ey est rapide et précis et de plus la méthode de Newton
``corrige'' les erreurs intermédiaires.
Nous sommes donc en mesure de calculer précisément le logarithme
ln(1 + x) pour disons | x| < 1/2. Pour calculer ln sur
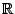 +,
on se ramène à [1, 2] en utilisant l'écriture
mantisse-exposant, puis si
x
+,
on se ramène à [1, 2] en utilisant l'écriture
mantisse-exposant, puis si
x 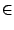 [3/2, 2] on peut en prendre la racine
carrée pour se retrouver dans l'intervalle souhaité.
On peut aussi effectuer une division par
[3/2, 2] on peut en prendre la racine
carrée pour se retrouver dans l'intervalle souhaité.
On peut aussi effectuer une division par 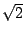 .
.
Remarquons que si x est connu à une erreur relative
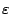 près, comme
près, comme
ln(
x(1±
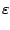
)) = ln(
x) + ln(1±
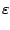
)
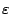 )|
)| 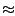
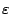 . Si ln(x) est proche
de 0, on a une grande perte de précision relative.
. Si ln(x) est proche
de 0, on a une grande perte de précision relative.
Finalement, nous savons calculer ln et exp sous réserve
d'avoir dans une table la valeur de ln(2). Pour calculer
ln(2) précisément, on peut utiliser
ln(2) = - ln(1/2) = - ln(1 - 1/2)
et le développement en série calculé en mode exact avec des
fractions à un ordre suffisant, on majore le reste en utilisant
que le terme général de la série ln(1 + x) est borné par
M = 1 en x = 1, donc d'après (3) :
|
Rn|
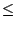
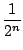
a:=sum((1/2)^k/k,k=1..80)|
puis la division en base 2 avec 81 bits de précision
iquo(numer(a)*2^81,denom(a))
Exercice : pour les fonctions trigonométriques, il faut une
méthode de calcul de  . On peut par exemple faire le calcul
de
16 arctan(1/5) - 4 arctan(1/239) en utilisant le développement
de la fonction arctan à un ordre suffisant.
. On peut par exemple faire le calcul
de
16 arctan(1/5) - 4 arctan(1/239) en utilisant le développement
de la fonction arctan à un ordre suffisant.



suivant: Autres applications
monter: Développement de Taylor, séries
précédent: Série alternée
Index
Retour à la page principale de mat249
![]() )/ln(2) termes ce qui est mieux, mais encore
relativement grand (par exemple
50 termes environ pour une précision en 1e - 16,
13 termes pour 1e - 4).
On a donc intérêt à se
ramener si possible à calculer la fonction en un x où la
convergence est plus rapide (donc | x| le plus petit possible).
Par exemple pour le calcul de ln(1 + x) on peut :
)/ln(2) termes ce qui est mieux, mais encore
relativement grand (par exemple
50 termes environ pour une précision en 1e - 16,
13 termes pour 1e - 4).
On a donc intérêt à se
ramener si possible à calculer la fonction en un x où la
convergence est plus rapide (donc | x| le plus petit possible).
Par exemple pour le calcul de ln(1 + x) on peut :
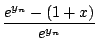
![]() +,
on se ramène à [1, 2] en utilisant l'écriture
mantisse-exposant, puis si
x
+,
on se ramène à [1, 2] en utilisant l'écriture
mantisse-exposant, puis si
x ![]() [3/2, 2] on peut en prendre la racine
carrée pour se retrouver dans l'intervalle souhaité.
On peut aussi effectuer une division par
[3/2, 2] on peut en prendre la racine
carrée pour se retrouver dans l'intervalle souhaité.
On peut aussi effectuer une division par ![]() .
.
![]() près, comme
près, comme
![]() . On peut par exemple faire le calcul
de
16 arctan(1/5) - 4 arctan(1/239) en utilisant le développement
de la fonction arctan à un ordre suffisant.
. On peut par exemple faire le calcul
de
16 arctan(1/5) - 4 arctan(1/239) en utilisant le développement
de la fonction arctan à un ordre suffisant.