


suivant: La fonction logarithme
monter: Développement de Taylor, séries
précédent: Séries entières.
Index
Série alternée
Théorème 6
Soit
Sn =  (- 1)kuk la somme jusqu'au rang n d'une
série de réels tels que la suite des uk décroit à partir
d'un rang n0 et tend vers 0
lorsque
k
(- 1)kuk la somme jusqu'au rang n d'une
série de réels tels que la suite des uk décroit à partir
d'un rang n0 et tend vers 0
lorsque
k  +
+ 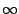 . Alors Sn converge vers une limite
S. Si n
. Alors Sn converge vers une limite
S. Si n 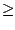 n0, la limite est comprise entre deux sommes
partielles succesives Sn et Sn+1 et le reste est majoré par
la valeur absolue du premier terme non sommé :
n0, la limite est comprise entre deux sommes
partielles succesives Sn et Sn+1 et le reste est majoré par
la valeur absolue du premier terme non sommé :
|
Rn|
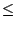
|
un+1|
Démonstration :
on montre que les suites
vn = S2n et
wn = S2n+1 sont
adjacentes. On a
vn+1 -
vn =
S2n+2 -
S2n = (- 1)
2n+2u2n+2 + (- 1)
2n+1u2n+1 =
u2n+2 -
u2n+1 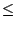
0
donc vn est décroissante, de même wn est croissante,
et
vn - wn = u2n+1 est positif et tend vers 0. On en déduit que
vn et wn convergent vers la même limite S telle que
vn > S > wn et les inégalités du théorème s'en déduisent.
Remarque
lorsqu'on utilise une suite alternée pour
trouver une valeur approchée, il faut que un tende assez
vite vers 0, sinon il y aura perte de précision sur la mantisse
lorsqu'on effectuera
u2n - u2n+1. On sommera aussi les termes
par ordre décroissant pour diminuer les erreurs d'arrondi.



suivant: La fonction logarithme
monter: Développement de Taylor, séries
précédent: Séries entières.
Index
Retour à la page principale de mat249
 | un+1|
| un+1|