


suivant: Polynômes : arithmétique, factorisation, interpolation
monter: Développement de Taylor, séries
précédent: La fonction logarithme
Index
On peut calculer certaines intégrales de la même manière,
par exemple
On peut aussi appliquer les techniques ci-dessus pour calculer
des solutions de certaines équations différentielles dont les
solutions ne s'expriment pas à l'aide des fonctions usuelles,
on remplace dans l'équation la fonction inconnue par son
développement en séries et on cherche une relation de récurrence
entre an+1 et an. Si on arrive à montrer par exemple
qu'il y a une solution ayant un développement alternée,
ou plus générallement,
si on a une majoration
| an+1/an| < C, alors le reste de la
série entière est majoré par
| anxn|/(1 - | Cx|) lorsque
| x| < 1/C, on peut alors calculer des valeurs approchées
de la fonction solution à la précision souhaitée en utilisant
le développement en séries entières.
Exemple : les fonctions de Bessel.
Soit m un entier positif fixé, on considère l'équation
différentielle
x2y'' + xy' + (x2 - m2)y = 0
dont on cherche une solution série entière
y = 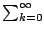 akxk. En remplacant dans l'équation, si
x est dans le rayon de convergence de la série (rayon supposé
non nul), on obtient
akxk. En remplacant dans l'équation, si
x est dans le rayon de convergence de la série (rayon supposé
non nul), on obtient
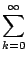 k
k(
k - 1)
akxk +
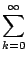 kakxk
kakxk +
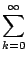
(
x2 -
m2)
akxk = 0
soit encore
| 0 |
= |
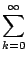 (k2 - m2 + x2)akxk (k2 - m2 + x2)akxk |
|
| |
= |
- m2a0 + (1 - m2)a1x + 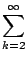 [(k2 - m2)ak + ak-2]xk [(k2 - m2)ak + ak-2]xk |
|
Par exemple, prenons le cas m = 0. On a alors a0 quelconque, a1
nul et pour k 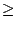 2
2
ak = -
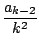
Donc tous les a d'indice impair sont nuls. Les pairs sont non nuls
si a0 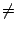 0, et ils sont de signe alterné.
Soit x fixé, on observe que pour 2k > | x|,
0, et ils sont de signe alterné.
Soit x fixé, on observe que pour 2k > | x|,
| a2kx2k| < | a2k-2x2k-2|
donc la série
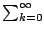 akxk est alternée à partir
du rang partie entière de | x| plus un. Donc elle converge pour
tout x (le rayon de convergence de y est +
akxk est alternée à partir
du rang partie entière de | x| plus un. Donc elle converge pour
tout x (le rayon de convergence de y est + 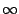 )
et le reste de la somme jusqu'à l'ordre 2n est
inférieur en valeur absolue à :
)
et le reste de la somme jusqu'à l'ordre 2n est
inférieur en valeur absolue à :
|
R2n(
x)|
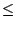
|
a2n+2x2n+2|
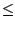 1, on calcule
y =
1, on calcule
y = 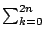 akxk,
on s'arrête au rang n tel que
akxk,
on s'arrête au rang n tel que
|
a2n+2x2n+2|
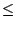
|
a2n+2|
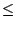
10
-10
a2n =
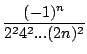
=
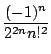
donc n = 7 convient.
Pour m 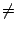 0, on peut faire un raisonnement analogue (les
calculs sont un peu plus compliqués).
0, on peut faire un raisonnement analogue (les
calculs sont un peu plus compliqués).
On a ainsi trouvé une solution y0 de l'équation
différentielle de départ dont on peut facilement calculer
une valeur approchée (aussi facilement que par exemple la fonction sinus
pour
| x| 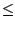 1),
on peut alors trouver toutes les solutions de l'équation
différentielle (en posant y = y0z et en cherchant z).
1),
on peut alors trouver toutes les solutions de l'équation
différentielle (en posant y = y0z et en cherchant z).



suivant: Polynômes : arithmétique, factorisation, interpolation
monter: Développement de Taylor, séries
précédent: La fonction logarithme
Index
Retour à la page principale de mat249
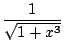
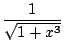
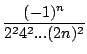 =
= 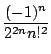
![]() 0, on peut faire un raisonnement analogue (les
calculs sont un peu plus compliqués).
0, on peut faire un raisonnement analogue (les
calculs sont un peu plus compliqués).
![]() 1),
on peut alors trouver toutes les solutions de l'équation
différentielle (en posant y = y0z et en cherchant z).
1),
on peut alors trouver toutes les solutions de l'équation
différentielle (en posant y = y0z et en cherchant z).