


suivant: Série alternée
monter: Développement de Taylor, séries
précédent: La fonction exponentielle
Index
Séries entières.
Les séries de type prendre la limite lorsque n tend vers
l'infini du développement de Taylor en x=0 sont de la forme
On peut s'intéresser plus générallement à
 anxn
lorsque an est un complexe quelconque,
c'est ce qu'on appelle une série entière, on peut aussi les voir comme
des polynômes généralisés.
anxn
lorsque an est un complexe quelconque,
c'est ce qu'on appelle une série entière, on peut aussi les voir comme
des polynômes généralisés.
S'il existe un point x0 tel que
| anx0n| est borné (ce sera le cas en particulier
si la série converge en x0), alors
|
anxn| = |
anx0n||
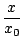
|
n 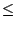 M
M|
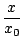
|
n
|
Rn|
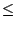 M
M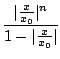
Théorème 5
S'il existe un rang n0, un réel M > 0 et un complexe x0 tels que
pour n > n0, on ait :
|
anx0|
n 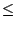 M
M
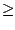 n0, on a :
n0, on a :
| Rn| 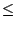 M M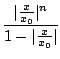 |
(3) |
On en déduit qu'il existe un réel
positif R 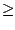 0 éventuellement égal à +
0 éventuellement égal à + 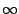 tel que
la série converge (la limite de la somme jusqu'à l'infini existe)
lorsque | x| < R et n'existe pas lorsque
| x| > R, ce réel est appelé rayon de convergence de la série.
Par exemple ce rayon vaut +
tel que
la série converge (la limite de la somme jusqu'à l'infini existe)
lorsque | x| < R et n'existe pas lorsque
| x| > R, ce réel est appelé rayon de convergence de la série.
Par exemple ce rayon vaut + 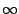 pour l'exponentielle, le sinus
ou le cosinus. Il
est égal à 1 pour la série géométrique
pour l'exponentielle, le sinus
ou le cosinus. Il
est égal à 1 pour la série géométrique  xn (car elle diverge
si | x| > 1 et converge si | x| < 1).
On ne peut pas dire ce qui se passe génériquement lorsqu'on
est à la limite, c'est-à-dire lorsque | x| = R (si
R
xn (car elle diverge
si | x| > 1 et converge si | x| < 1).
On ne peut pas dire ce qui se passe génériquement lorsqu'on
est à la limite, c'est-à-dire lorsque | x| = R (si
R 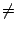 +
+ 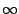 ). Mais cela n'a en fait pas trop d'importance en pratique
car même si la série converge, elle converge souvent trop lentement
pour donner de bonnes approximations. En fait, la vitesse de
convergence d'une série entière de rayon
R
). Mais cela n'a en fait pas trop d'importance en pratique
car même si la série converge, elle converge souvent trop lentement
pour donner de bonnes approximations. En fait, la vitesse de
convergence d'une série entière de rayon
R 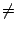 +
+ 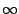 est
en gros la même que celle d'une série géométrique de raison | x|/R.
est
en gros la même que celle d'une série géométrique de raison | x|/R.
Lorsque 2 séries ont un rayon de convergence non nul, alors on
peut effectuer leur somme, leur produit comme des polynômes et la
série somme/produit a un rayon de convergence au moins égal au plus
petit des 2 rayons de convergence des arguments. On peut inverser une série
entière non nulle en 0 en appliquant
(1 + x)-1 = 1 - x + x2 - x3 + ...
et on obtient une série entière de rayon de
convergence non nul. On peut aussi composer deux séries entières
g et f en gof (avec les règles de calcul de composition
des polynômes) si f (0) = 0. On peut enfin dériver
et intégrer une série entière terme à terme dans son rayon de convergence.
On dit qu'une fonction est développable en série entière en 0 si
elle est égale à son développement de Taylor en 0 sommé jusqu'en l'infini
dans un disque de centre 0 et de rayon non nul. Les fonctions
exponentielle, sinus, cosinus sont donc développables en série entière en 0.
La fonction tangente également car le dénominateur cosinus est non nul en 0,
mais son rayon de convergence n'est pas l'infini et le calcul des an
est assez complexe.
La fonction
(1 + x)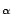 est développable en séries entières
pour tout
est développable en séries entières
pour tout
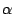
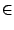
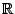 avec un rayon de convergence 1 (ou l'infini
pour
avec un rayon de convergence 1 (ou l'infini
pour 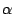 entier positif).
entier positif).
(1 +
x)
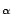
= 1 +
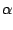 x
x +
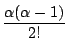 x2
x2 + ... +
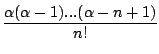 xn
xn + ...
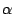 = - 1, c'est la série
géométrique de raison - x, en effet si | x| < 1 :
En intégrant par rapport à x, on obtient que ln(1 + x) est développable
en série entière en 0 de rayon de convergence 1 et
= - 1, c'est la série
géométrique de raison - x, en effet si | x| < 1 :
En intégrant par rapport à x, on obtient que ln(1 + x) est développable
en série entière en 0 de rayon de convergence 1 et
ln(1 +
x) =
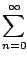
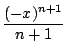
arctan(
x) =
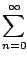
(- 1)
n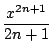
,



suivant: Série alternée
monter: Développement de Taylor, séries
précédent: La fonction exponentielle
Index
Retour à la page principale de mat249
![$\displaystyle {\frac{{f^{[n]}(0)}}{{n!}}}$](img83.png)
![$\displaystyle {\frac{{f^{[n]}(0)}}{{n!}}}$](img83.png)
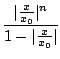
![]() 0 éventuellement égal à +
0 éventuellement égal à + ![]() tel que
la série converge (la limite de la somme jusqu'à l'infini existe)
lorsque | x| < R et n'existe pas lorsque
| x| > R, ce réel est appelé rayon de convergence de la série.
Par exemple ce rayon vaut +
tel que
la série converge (la limite de la somme jusqu'à l'infini existe)
lorsque | x| < R et n'existe pas lorsque
| x| > R, ce réel est appelé rayon de convergence de la série.
Par exemple ce rayon vaut + ![]() pour l'exponentielle, le sinus
ou le cosinus. Il
est égal à 1 pour la série géométrique
pour l'exponentielle, le sinus
ou le cosinus. Il
est égal à 1 pour la série géométrique ![]() xn (car elle diverge
si | x| > 1 et converge si | x| < 1).
On ne peut pas dire ce qui se passe génériquement lorsqu'on
est à la limite, c'est-à-dire lorsque | x| = R (si
R
xn (car elle diverge
si | x| > 1 et converge si | x| < 1).
On ne peut pas dire ce qui se passe génériquement lorsqu'on
est à la limite, c'est-à-dire lorsque | x| = R (si
R ![]() +
+ ![]() ). Mais cela n'a en fait pas trop d'importance en pratique
car même si la série converge, elle converge souvent trop lentement
pour donner de bonnes approximations. En fait, la vitesse de
convergence d'une série entière de rayon
R
). Mais cela n'a en fait pas trop d'importance en pratique
car même si la série converge, elle converge souvent trop lentement
pour donner de bonnes approximations. En fait, la vitesse de
convergence d'une série entière de rayon
R ![]() +
+ ![]() est
en gros la même que celle d'une série géométrique de raison | x|/R.
est
en gros la même que celle d'une série géométrique de raison | x|/R.
![]() est développable en séries entières
pour tout
est développable en séries entières
pour tout
![]()
![]()
![]() avec un rayon de convergence 1 (ou l'infini
pour
avec un rayon de convergence 1 (ou l'infini
pour ![]() entier positif).
entier positif).
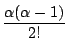 x2 + ... +
x2 + ... + 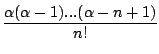 xn + ...
xn + ...
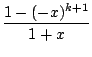
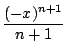
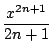 ,
,