comme géodésique reliant les deux puits, on
montrera que l'on peut ainsi rendre l'intégrale de (24)
non multiple de 
. Il reste alors à modifier W près des
éventuelles autres géodésiques minimales de W pour que soit l'unique géodésique minimale de V reliant les deux puits.
On va utiliser des coordonnées de Gauß:
Preuve:
Soit f une fonction de 
périodique
sur 
, on pose:
On paramètre de telle sorte que
soit solution d'énergie nulle des équations de Hamilton pour
:
Soit 
défini par:
Si on paramètre par s, on a:
On pose donc:
On a alors:
Regardons la deuxième équation
canonique que l'on doit vérifier pour que 
soit
géodésique d'Agmon pour le potentiel V:
On a:
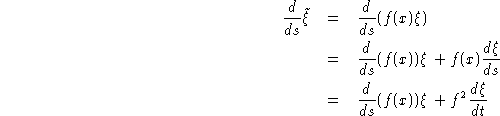
D'autre part:
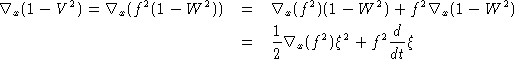
Le long de , l'équation (26) équivaut donc à:
L'équation (27) entraine:
le long de . Réciproquement si 
est
parallèle à 
, alors en faisant le produit scalaire de
(27) avec on obtient:
soit:
qui est clairement vérifiée.
Donc est une géodésique pour la distance d'Agmon
associée à W si et seulement si est tangent à
le long de .
On observe maintenant que la distance d'Agmon d(x,P ) de x au
puits P (pour W) est une fonction dont le gradient est
tangent aux géodésiques d'Agmon issues de P . Soit 
un voisinage du puits P sur lequel d(x,P ) est
(analytique en fait), on prendra pour une
boule de rayon 
pour la distance d'Agmon induite par
W. Soit alors g une fonction de 
telle que:
Si on pose:
sur , alors f se prolonge en une fonction
et périodique dont le gradient est parallèle aux géodésiques
issues de P . On remarque que les géodésiques d'Agmon pour
V et W issues de P sont identiques. Comme est minimale
pour W, elle le reste pour V. En effet, la V-longueur d'Agmon
d'une géodésique issue de P de W-longueur d'Agmon l est:
L'ensemble des géodésiques minimales n'est donc pas modifié.
Montrons qu'on peut choisir g pour que l'intégrale de
(24) ne soit pas un multiple de . On note L la
longueur euclidienne de de sorte que l'intégrale de
(24) s'écrit pour W
et devient pour V :
puisque le support géométrique de la géodésique reste identique. Rappelons que:
On en déduit les inégalités suivantes dans un voisinage du puits P:
avec égalité si et seulement si f=1. Comme la courbure 
est non plate au puits, il existe 
(assez petit) tel que
garde un signe constant sur l'intervalle 
, pour
fixer les idées on supposera que 
. Quitte à diminuer
ou 
, on peut aussi supposer que 
.
On a alors:
avec égalité si
et seulement si 
sur 
. Comme g=1
en-dehors de l'intervalle , on a:
donc la différence entre les
deux intégrales (29) et (28) est positive, et
même strictement positive si g ne vaut pas identiquement 1. De
plus cette différence peut être rendue aussi petite que l'on veut
en choisissant une fonction g assez proche de 1. On peut donc
choisir g pour que l'intégrale (29) ne soit pas un
multiple de .
