Dérivée de Lie.

  La donnée d'un champ de vecteurs v^a définit un groupe à un paramètre de difféomorphismes, le flot de v^a, tel que:

C'est-à-dire que la courbe paramétrée par t admet comme vecteur vitesse à l'instant t le vecteur v^a (figure 4, p. ).

  
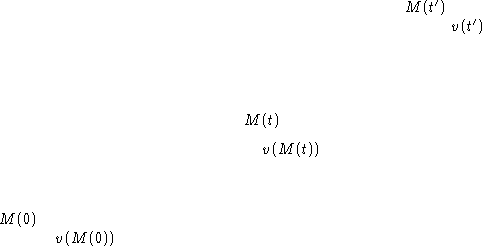
Figure: Le flot d'un champ de vecteur.

 

 

Exemple: dérivée de Lie selon v d'un champ de vecteur w. Graphiquement, on représente le champ de vecteurs w au point M par , on suit alors le flot de v en partant du point M et du point , ce qui déforme le vecteur w (figure 5, p. ). (Bien entendu, il faut choisir le point très voisin de M dans la direction de w(M)).

  
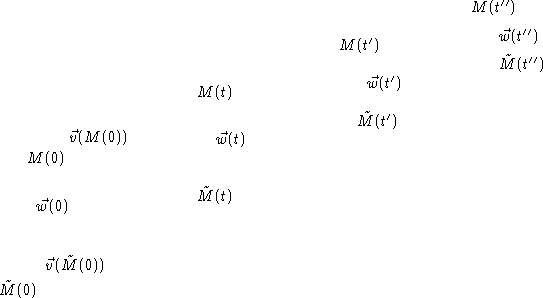
Figure: Transformation d'un vecteur le long du flot d'un autre champ de vecteurs.

Calculons en coordonnées locales . On a:

Donc:

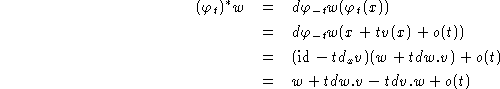
et:

ou en coordonnées:

finalement la dérivée de Lie d'un champ de vceteur est égale au crochet de Lie de ce champ de vecteurs avec le champ par rapport auquel on dérive: