Opérateur d.

  Si on se donne , alors , on peut aussi voir df comme une section de T^*M. On passe ainsi d'une forme différentielle de degré 0 à une forme différentielle de degré 1. On va généraliser l'opérateur d à toutes les formes différentielles.

   

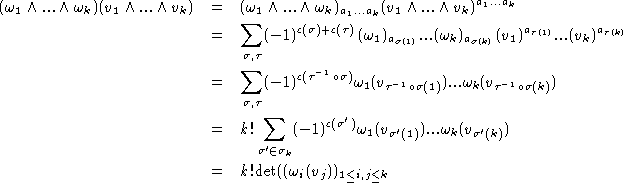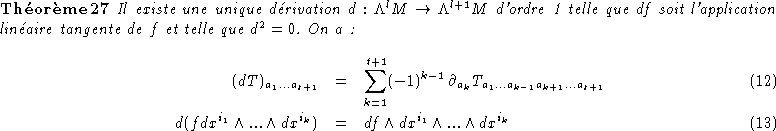
Preuve:
Commençons par l'unicité. Si d et d' satisfont aux exigences du théorème, alors d=d' sur les fonctions, de plus

car d²=d'²=0. Puis:

donc d'=d car tout tenseur antisymétrique est localement combinaison linéaire finie de tenseur du type . Il suffit donc de prouver l'existence locale de d, donc de vérifier que la formule (12) définit une dérivation d'ordre 1 telle que d²=0.

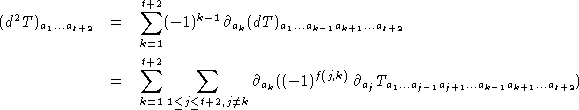
où f(j,k)=j-1 si j<k et f(j,k)=j-2 si j>k. Ce qui donne d²T=0 car les termes (j,k) et (k,j) de la somme s'annulent.

Dernier point à vérifier: d est une dérivation d'ordre 1, i.e.

Pour simplifier les notations, on adopte la convention que si on recouvre par le signe un indice d'un ensemble d'indice, c'est qu'il faut le retirer de l'ensemble d'indice, par exemple:

On a alors:

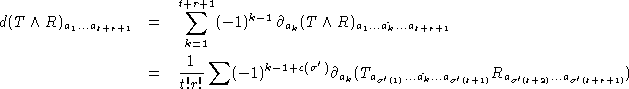
où la somme porte sur et . Remarquons que si , il faut décaler les indices du terme général de la somme en:

On peut décomposer ce terme général en deux, en faisant porter la dérivation sur T ou sur R. Il s'agit d'identifier avec dans le premier cas et avec dans le second. Or:

où la somme porte sur et sur . A un tel couple , nous allons faire correspondre un triplet où est une permutation fixant k, qu'on identifie naturellement avec une permutation de : on pose et de telle sort que:

Comme est un cycle de longueur donc

Le terme général de la somme de devient si k>t+1

Si , le terme général s'écrit:

On déplace ensuite le trou à sa place entre et , on constate que ce terme général ne dépend plus de , on somme donc par rapport à qui donne un facteur t+1 que l'on simplifie avec 1/(t+1)! en 1/t! et on obtient le terme général de la somme de lorsqu'on fait porter la dérivation sur T.

De même,

où la somme porte sur et sur . On effectue la même correspondance que ci-dessus, on obtient donc le terme général de lorsqu'on fait porter la dérivation sur R multiplié par (-1)^t.

Exercices

1. Par l'argument d'unicité, on sait que si on change de base la formule (12) détermine l'action de d dans la nouvelle base. (Ceci justifie a postériori l'utilisation de lettres romaines dans la démonstration de l'existence locale de d alors qu'on aurait dû utiliser des lettres grecques). Vérifiez le directement.
2. Montrer que i(v)d+di(v) est une dérivation d'ordre 0. Plus généralement si D et D' sont deux dérivations d'ordre respectifs r et r', montrer que:

   

   est une dérivation d'ordre r+r'.

   Montrer que si deux dérivations d'ordre supérieur ou égal à -1 coincident sur les fonctions et sur les 1-formes, alors elles coincident sur toutes les formes différentielles. Montrer que si deux dérivations d'ordre positif coincident sur les fonctions et commutent avec d alors elles sont égales.

3. On définit le produit extérieur de vecteurs comme celui des 1-formes. Montrer que

   

Solution du 3eme exercice:
On a:

et l'analogue pour le k-vecteur:

donc: