![]()
où l'on a fait k produits de T*mM et l produits
de TmM. On appelle tenseur de type (k,l) la donnée d'une
application ![]() et multilinéaire de T(k,l)M sur
et multilinéaire de T(k,l)M sur ![]() (i.e. linéaire par rapport à chaque T*mM
et à chaque TmM). Par dualité, un tenseur de type (k,l)
est une section de
(i.e. linéaire par rapport à chaque T*mM
et à chaque TmM). Par dualité, un tenseur de type (k,l)
est une section de
![]()
les champs de vecteurs sont des tenseurs de type (1,0) et les champs de 1-forme des tenseurs de type (0,1). Les tenseurs de type (k,0) sont dits contravariants, ceux de type (0,l) sont dits covariants.
A l'aide d'un tenseur de type (k,l) et d'un tenseur de type (k',l') on peut construire un tenseur de type (k+k',l+l') en en faisant le produit (tensoriel). Grâce à la linéarité, tout tenseur de type (k,l) est une somme de produits tensoriels de k champs de vecteurs par l 1-formes, donc la dimension de T(k,l)mM est nk+l, puisque si T est un tenseur de type (k,l), il existe nk+l réels tels que (en coordonnées locales):
Lorsqu'on change de systèmes de coordonnées, on obtient les nouvelles composantes en fonction des anciennes en appliquant les formules de changement de coordonnées pour les champs de vecteurs et de 1-formes (4) et (5) dans (7):
![]()
Les composantes d'un tenseur T de type (k,l) sont donc les
![]()
avec ![]() .
.
Convention:
Lorsqu'on a des égalités entre composantes de tenseurs,
on utilise des lettres romaines comme
indice si l'égalité est valable dans tout système de coordonnées
(c'est alors une égalité entre tenseurs) et des lettres grecques
si l'égalité n'est valable que dans un système de coordonnées.
Par exemple, considérons le tenseur
![]() , on a:
, on a:
![]()
car l'égalité composante par composante est vraie dans n'importe quel système de coordonnées, pas seulement dans le système (x1,...,xn). Par contre, l'égalité
![]()
n'est vraie que dans le système de coordonnées (x1,...,xn) car ce n'est que dans ce système que toutes les composantes de ce tenseur sont 0 ou 1, donc on utilise les lettres grecques.
On adopte donc pour un champ de vecteur la notation vc et pour un champ de 1-formes wc .
En coordonnées, on a:
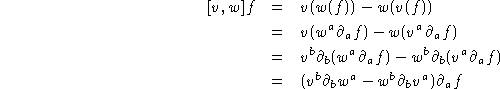
donc: