Espace cotangent.

  Soit . On définit l'espace cotangent en m à M:

c'est également le dual de T_mM car toute forme linéaire de T_mM est la différentielle d'une fonction (il suffit de le montrer en coordonnées locales, et dans le cas d'un ouvert de , il suffit de prendre pour f la forme linéaire elle-même).

  
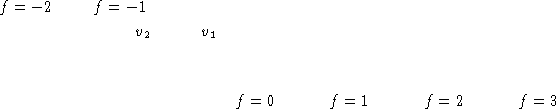
Figure: Représentation d'une 1-forme dans .

On représente la forme linéaire par ses lignes de niveaux (cf. figure 2, ). La valeur de la forme linéaire sur un vecteur se calcule en regardant à quelle courbe de niveau appartient l'extrémité du vecteur. Ici f(v₂)=0 et .

 

Preuve:
Soit O un ouvert de M contenant m, source de la carte locale x à valeurs dans l'ouvert . On en déduit une carte locale dite carte naturelle de T^*M définie sur :

Il reste à vérifier que deux cartes naturelles sont compatibles sur leur domaine commun de définition. Soit donc y une autre carte de M et déterminons . Soit , (m,d_mf) son image réciproque par T^*x, et l'image de (m,d_mf) par T^*y. On a:

Comme les cartes x et y sont compatibles, est . Il reste à exprimer de manière en fonction de et de x(m). Pour cela, on utilise la linéarité de d_mf et le changement de carte pour un vecteur tangent (4):

d'où l'on tire:

ou encore:

qui est bien une fonction de et de m.