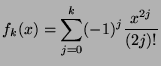suivant: D'autres applications
monter: Les séries entières
précédent: Rappels du cours
Exercice 1 (à rendre à la fin de la 1ère séance de ce TP)
Écrire 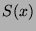 , le développement en
séries entières au voisinage de
, le développement en
séries entières au voisinage de  de
de 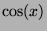 .
.
Tracer sur un même graphique les graphes des fonctions suivantes :
Graphiquement on voit que 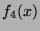 approche
approche 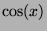 : sur quel intervalle
cette approximation vous paraît-elle acceptable ?
: sur quel intervalle
cette approximation vous paraît-elle acceptable ?
Donner une majoration du reste 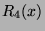 de cette série
de cette série 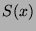 .
De façon plus précise,
.
De façon plus précise, 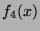 approche
approche 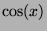 pour
pour
![$ x \in [-1,1]$](img50.png) avec quelle erreur ?
avec quelle erreur ?
En déduire un encadrement de 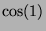 .
.
Exercice 2 (à rendre à la fin de la 1ère séance de ce TP)
On veut approcher sur l'intervalle ![$ [0;\pi]$](img52.png)
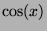 à
à 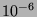 près
par son développement en séries entières au voisinage de
près
par son développement en séries entières au voisinage de  .
Déterminer le plus petit
.
Déterminer le plus petit 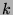 pour que :
pour que :
réalise cette approximation.
Calculer avec cette méthode  , puis calculer
, puis calculer
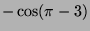 en
utilisant une valeur approchée de
en
utilisant une valeur approchée de  à
à 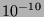 près.
près.
Comparez les approximations obtenues.



suivant: D'autres applications
monter: Les séries entières
précédent: Rappels du cours
2003-02-19
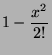
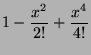
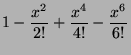
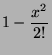
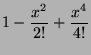
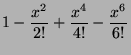
![]()
![]() à
à ![]() près
par son développement en séries entières au voisinage de
près
par son développement en séries entières au voisinage de ![]() .
Déterminer le plus petit
.
Déterminer le plus petit ![]() pour que :
pour que :