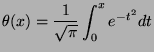suivant: Les séries de Fourier
monter: Les séries entières
précédent: Exercices
Exercice 3 (à rendre au début du TP5)
On veut calculer
Écrire le développement en séries entières au voisinage de  de :
Écrire
de :
Écrire 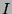 sous la forme d'une série de terme général
sous la forme d'une série de terme général  .
.
Soit 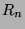 le reste de cette série :
trouver une majoration de
le reste de cette série :
trouver une majoration de 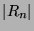 .
Quelle est l'aproximation obtenue pour la valeur de
.
Quelle est l'aproximation obtenue pour la valeur de 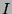 lorsqu'on utilise
comme approximation de
lorsqu'on utilise
comme approximation de
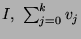 ? Donner un encadrement
de
? Donner un encadrement
de 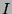 obtenu en prenant
obtenu en prenant  .
.
Exercice 4 (à rendre au début du TP5)
On veut calculer
Écrire le développement en séries entières au voisinage de  de :
Écrire
de :
Écrire 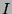 sous la forme d'une série de terme général
sous la forme d'une série de terme général 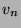 .
.
En déduire une valeur de 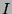 à
à 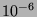 près.
près.
Exercice 5 (à rendre au début du TP5)
Écrire le développement en séries entières au voisinage de  de :
de :
En déduire une valeur de
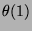 à
à 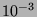 près.
près.
2003-02-19
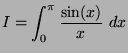
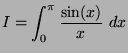
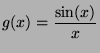
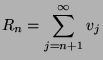
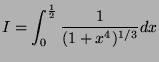
![]() de :
de :