




suivant: The function : Beta
monter: Real numbers
précédent: Complementary error function: erfc
Table des matières
Index
The 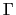 function : Gamma
function : Gamma
Gamma takes as argument a number a.
Gamma returns the value of the 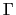 function in a, defined by :
function in a, defined by :
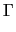
(
x) =
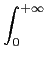 e-ttx-1dt
e-ttx-1dt, if
x > 0
If x is a positive integer, 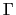 is computed by applying
the recurrence :
is computed by applying
the recurrence :
Hence :
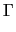
(
n + 1) =
n!
Input :
Gamma(5)
Output :
24
Input :
Gamma(0.7)
Output :
1.29805533265
Input :
Gamma(-0.3)
Output :
-4.32685110883
Indeed : Gamma(0.7)=-0.3*Gamma(-0.3)
Input :
Gamma(-1.3)
Output :
3.32834700679
Indeed Gamma(0.7)=-0.3*Gamma(-0.3)=(-0.3)*(-1.3)*Gamma(-1.3)
giac documentation written by Renée De Graeve and Bernard Parisse