The integer Euclidean remainder : irem remain smod mods mod %

irem (or remain) returns the integer remainder r from the Euclidean division of two integers a and b given as arguments (a = b*q + r avec 0 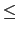$\leq$ r < b).
For Gaussian integers, we choose q so that b*q is as near by a as possible and it can be proved that r may be choosen so that | r|² 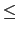$\leq$ | b|²/2.
Input :

irem(148,5)

Output :

3

irem works with long integers or with Gaussian integers.
Example :

irem(factorial(148),factorial(45)+2 )

Output :

111615339728229933018338917803008301992120942047239639312

Another example

irem(25+12*i,5+7*i)

Output :

-4+i

Here a - b*q = - 4 + i and | - 4 + i|² = 17 < | 5 + 7*i|²/2 = 74/2 = 37

smod or mods is a prefixed function and has two integers a and b as arguments.
smod or mods returns the symetric remainder s of the Euclidean division of the arguments a and b (a = b*q + s with - b/2 < s 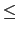$\leq$ b/2).
Input :

smod(148,5)

Output :

-2

mod (or %) is an infixed function and has two integers a and b as arguments.
mod (or %) returns r%b of Z/bZ where r is the remainder of the Euclidean division of the arguments a and b.
Input :

148 mod 5

or

148 % 5

Output :

3 % 5

Note that the answer 3 % 5 is not an integer (3) but an element of Z/5Z (see 1.31 to have the possible operations in Z/5Z).