The integer Euclidean quotient : iquo intDiv

iquo (or intDiv) returns the integer quotient q of the Euclidean division of two integers a and b given as arguments. (a = b*q + r with 0 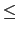$\leq$ r < b).
For Gaussian integers, we choose q so that b*q is as near by a as possible and it can be proved that r may be choosen so that | r|² 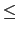$\leq$ | b|²/2.
Input :

iquo(148,5)

Output :

29

iquo works with integers or with Gaussian integers.
Input :

iquo(factorial(148),factorial(145)+2 )

Output :

3176375

Input :

iquo(25+12*i,5+7*i)

Output :

3-2*i

Here a - b*q = - 4 + i and | - 4 + i|² = 17 < | 5 + 7*i|²/2 = 74/2 = 37