Define a polynomial P(x) =
- Compute the values of P(x) at
x = ak =This is just the discrete Fourier transform of c since
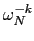 = exp(
= exp(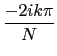 ), k = 0..N - 1
P(ak) =Input, for example :
), k = 0..N - 1
P(ak) =Input, for example :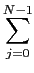 cj(
cj(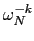 )j = FN(c)k
P(x):=x+xHere the coefficients of P are [0,1,1,0], N = 4 and
)j = FN(c)k
P(x):=x+xHere the coefficients of P are [0,1,1,0], N = 4 and^2; w:=i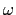 = exp(2i
= exp(2i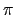 /4) = i.
/4) = i.
Input :
fft([0,1,1,0])
Output :
[2,-1-i,0,-1+i]
hence- P(0)=2,
- P(-i)=P(w
^-1)=-1-i, - P(-1)=P(w
^-2)=0, - P(i)=P(w
^-3)=-1+i.
- Compute the values of P(x) at
x = bk =This is N times the inverse fourier transform of c since
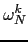 = exp(
= exp(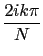 ), k = 0..N - 1
P(ak) =Input, for example :
), k = 0..N - 1
P(ak) =Input, for example :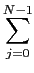 cj(
cj(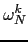 )j = NFN-1(c)k
)j = NFN-1(c)k
P(x):=x+x^2 and w:=i
Hence, the coefficients of P are [0,1,1,0], N = 4 and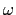 = exp(2i
= exp(2i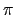 /4) = i.
/4) = i.
Input :
4*ifft([0,1,1,0])
Output :
[2,-1+i,0,-1-i]
hence :- P(0)=2,
- P(i)=P(w
^1)=-1+i, - P(-1)=P(w
^2)=0, - P(-i)=P(w
^3)=-1-i.
Let f be periodic function of period 2
p(x) = 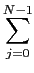 pjexp(ijx), p(xk) = fk
pjexp(ijx), p(xk) = fk
Replacing xk by it's value in p(x) we get:
(pk) = 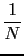 FN( (fk) )
FN( (fk) )
If the function f is real,
p-k = | p(x) | = | p0 +2 |
|
| p(x) | = | p0 +2 |
Let f be a periodic function of period 2
f (xk) = yk, xk = 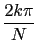 , k = 0..N - 1
, k = 0..N - 1
Suppose that the Fourier serie of f converges to f (this will
be the case if for example f is continuous). If N is large,
a good approximation of f will be given by:
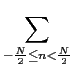 cnexp(inx)
cnexp(inx)
cn = 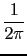
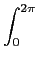 f (t)exp(- int)dt
f (t)exp(- int)dt
The numeric value of the integral
| f (xk)exp(- inxk) | = | ykexp(- 2i |
|
| f (0)exp(0) = f (2 |
= | y0 = yN |
Hence :
[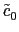 ,..
,..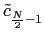 ,
,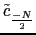 ,..c-1] =
,..c-1] = 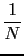 FN([y0, y1...y(N-1)])
FN([y0, y1...y(N-1)])
since
- if n
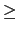 0,
0,
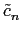 = yn
= yn
- if n < 0
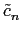 = yn+N
= yn+N
-
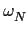 = exp(
= exp(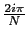 ),
then
),
then
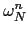 =
= 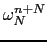
Properties
- The coefficients of the trigonometric polynomial that interpolates f
at x = 2k
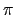 /N are
pn =
/N are
pn =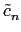 , -
, - 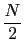
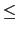 n <
n < 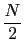
- If f is a trigonometric polynomial P of degree
m
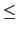
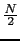 ,
then
f (t) = P(t) =the trigonometric polynomial that interpolate f = P is P, the numeric approximation of the coefficients are in fact exact (
,
then
f (t) = P(t) =the trigonometric polynomial that interpolate f = P is P, the numeric approximation of the coefficients are in fact exact (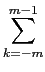 ckexp(2ik
ckexp(2ik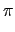 t)
t)
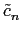 = cn).
= cn).
- More generally, we can compute
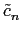 - cn.
- cn.
Suppose that f is equal to it's Fourier serie, i.e. that :f (t) =Then :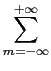 cmexp(2i
cmexp(2i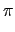 mt),
mt), 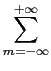 | cm| <
| cm| < 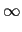 f (xk) = f (Replace yk by it's value in
f (xk) = f (Replace yk by it's value in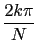 ) = yk =
) = yk = 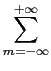 cm
cm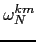 ,
, 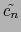 =
= 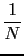
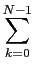 yk
yk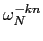
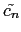 :
If m
:
If m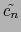 =
= 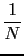
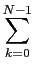
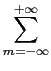 cm
cm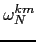
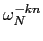
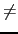 n(mod N),
n(mod N),
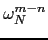 is a N-th root of unity different
from 1, hence:
Therefore, if m - n is a multiple of N ( m = n + l . N) then
is a N-th root of unity different
from 1, hence:
Therefore, if m - n is a multiple of N ( m = n + l . N) then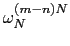 = 1,
= 1, 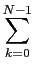
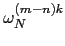 = 0
= 0
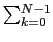
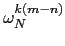 = N, otherwise
= N, otherwise
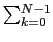
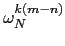 = 0.
By reversing the two sums, we get
= 0.
By reversing the two sums, we get
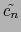
= 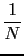
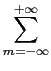 cm
cm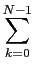
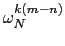
= 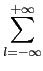 c(n+l . N)
c(n+l . N)= ...cn-2 . N + cn-N + cn + cn+N + cn+2 . N + .....
Conclusion: if | n| < N/2,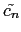 - cn is a sum of cj of large indices
(at least N/2 in absolute value), hence is small (depending on the
rate of convergence of the Fourier series).
- cn is a sum of cj of large indices
(at least N/2 in absolute value), hence is small (depending on the
rate of convergence of the Fourier series).
f(t):=cos(t)+cos(2*t)
x:=f(2*k*pi/8)$(k=0..7)
Output :
x:=f(2*k*pi/8)$(k=0..7)
fft(x)=[0.0,4.0,4.0,0.0,0.0,0.0,4.0,4.0]
c0 = 0, c1 = 4.0/8, c2 = 4.0/2, c3 = 0.0,
c-4 = 0, c-3 = 0, c-2 = 4.0/8, = c-1 = 4.0/8
Hence bk = 0 and
ak = c-k + ck is equal to 1 if k = 1, 2 and 0 otherwise.
c-4 = 0, c-3 = 0, c-2 = 4.0/8, = c-1 = 4.0/8
If P(x) =
P(x)Q(x) = 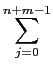 (a*b)jxj
(a*b)jxj
We compute FN(a), FN(b), then
ab = FN-1(FN(a) . FN(b))
using the properties
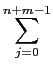 (a*b)jxj
(a*b)jxj
NFN(x . y) = FN(x)*FN(y), FN(x*y) = FN(x) . FN(y)