The properties of the Discrete Fourier Transform

The Discrete Fourier Transform F_N is a bijective transformation on periodic sequences such that

$$\omega_{N} {\frac{{1}}{{N}}} \omega_{N}^{{-1}}$$ =

$${\frac{{1}}{{N}}} \overline{{F_{N}}} \mathbb {C}$$ =

i.e. :

(F_N^-1(x))_k = $${\frac{{1}}{{N}}}$$$$\sum_{{j=0}}^{{N-1}}$$x_j$$\omega_{N}^{{k\cdot j}}$$

Inside Xcas the discrete Fourier transform and it's inverse are denote by fft and ifft:

fft(x)= F_N(x), ifft(x)= F_N^-1(x)

Definitions
Let x and y be two periodic sequences of period N.

• The Hadamard product (notation ^. ) is defined by:
  (x ^. y)_k = x_ky_k

• the convolution product (notation *) is defined by:
  (x*y)_k = 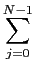$$\sum_{{j=0}}^{{N-1}}$$x_jy_k-j

Properties :

N*F_N(x ^. y) = F_N(x)*F_N(y)

F_N(x*y) = F_N(x) ^. F_N(y)