Fast Fourier Transform : fft

fft takes as argument a list (or a sequence) $\tt [a_0,..a_{N-1}]$ where N is a power of two.
fft returns the list $\tt [b_0,..b_{N-1}]$ such that, for k=0..N-1

$$\tt {fft([a_0,..a_{N-1}])}[k]=b_k=\sum_{j=0}^{N-1}x_j\omega_N^{-k\cdot j}$$

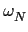where $\omega_{N}^{}$ is a primitive N-th root of the unity.
Input :

fft(0,1,1,0)

Output :

[2.0, -1-i, 0.0, -1+i]