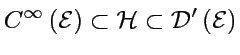
Il existe un espace de Hilbert
de distributions
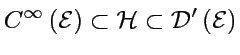
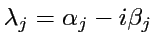 sont appelées ``résonances
de Ruelle''.
sont appelées ``résonances
de Ruelle''.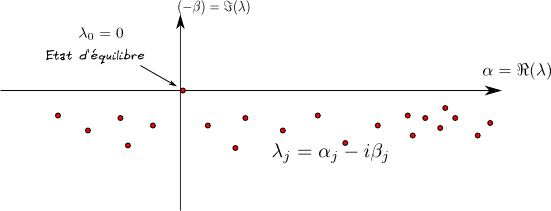
Notons la décomposition spectrale (si spectre simple):
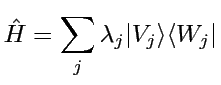
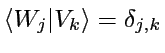 . En particulier
. En particulier 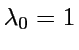 ,
,
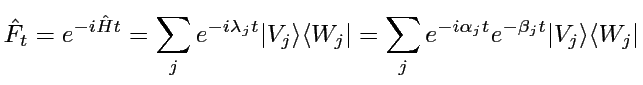
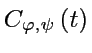 =
=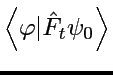
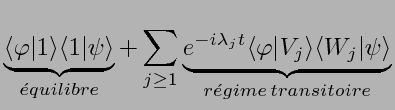
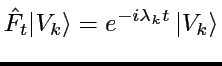
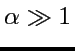 :
:
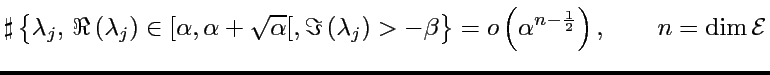
On a vu qu'une distribution 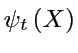 évolue
d'après
(2):
évolue
d'après
(2):
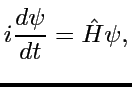 avec
avec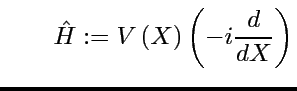
Afin de comprendre le spectre de ![]() (résonances de Ruelle),
pensons
(résonances de Ruelle),
pensons
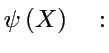 "fonction d'onde"
"fonction d'onde"
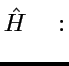 "opérateur Hamiltonien quantique"
"opérateur Hamiltonien quantique"
D'après le ``principe de correspondance'' le ``Hamiltonien classique'' est:
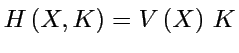
(rappel: on applique ![]() sur un mode de Fourier
sur un mode de Fourier 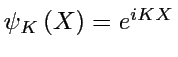 ),
avec
),
avec
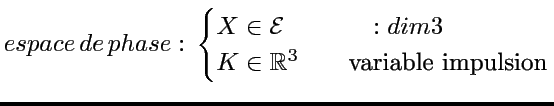
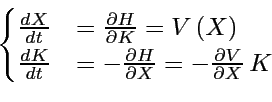
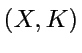 :
:
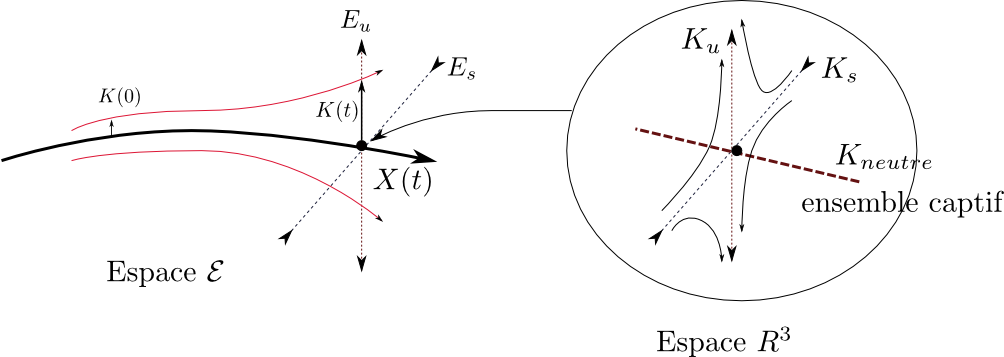
les trajectoires ont un comportement "simple": elles diffusent sur un ``ensemble captif''
et fuient
vers 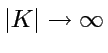 c'est à dire vers les
échelles
microscopiques.
c'est à dire vers les
échelles
microscopiques.
On peut maintenant comprendre les résonances de Ruelle.
Comme en phys. atomique
(ou autre "système quantique ouvert"), où une onde lumineuse diffuse
sur un atome
(dans l'espace réel), révélant des états métastables appelées ``résonances quantiques'',
dans le mécanisme de la fluorescence.
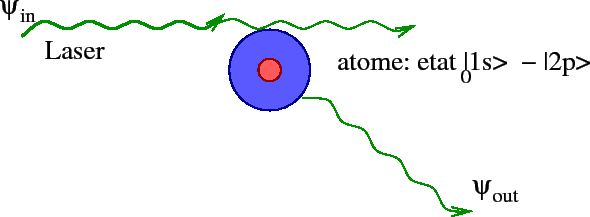

Il y a deux approches traditionelles pour la théorie de la diffusion. On utilise ici la 2ème.
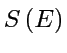 de
``Scattering'':
de
``Scattering'':Comme dans les expériences, on observe le système depuis l'infini.
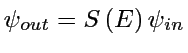
Ex: le modèle de Breit-Wigner d'une résonance isolée, donne une Lorentzienne
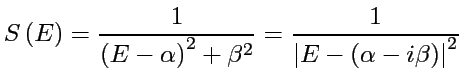
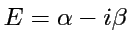 .
.

Dans certains espaces fonctionnels (distributions de Sobolev
Anisotropes),
une résonances est un état stationnaire ![]() :
:
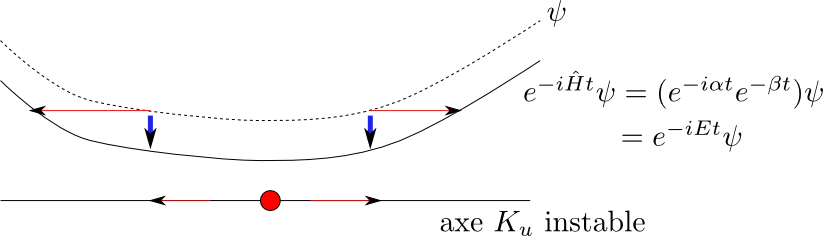
Dans ces espaces, le spectre de l'opérateur de transfert est discret, révélant une dynamique effective irréversible: on obtient ainsi le spectre de Ruelle.