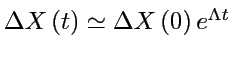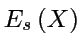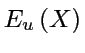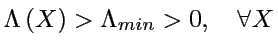Que veulent dire les mots ``déterministe''
et ``chaos''?
On observe un mouvement ``régulier'' et ``prévisible''.
- La loi
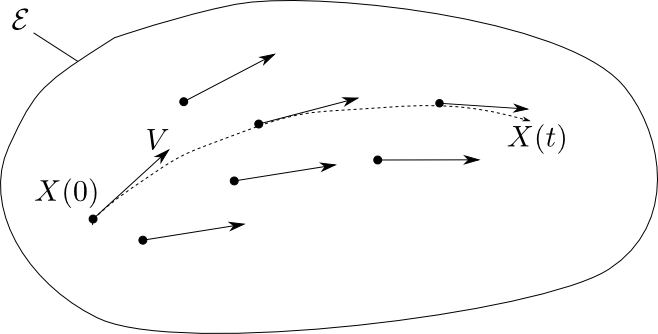
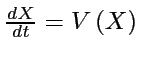 se représente par un champ
de vecteur
se représente par un champ
de vecteur 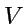 dans l'espace des états
dans l'espace des états
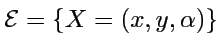 qui est de dim 3, et borné (c'est la ``couche d'énergie'').
qui est de dim 3, et borné (c'est la ``couche d'énergie'').
- Vision au début XIXeme siècle: Il semble que toute
la nature
soit régie par des lois déterministes.
 Laplace a écrit: ``.... En vertu du déterminisme universel,
l'intelligence qui connaîtrait avec une absolue précision la position
et la vitesse de tout objet dans la position initiale pourrait
calculer l'évolution de l'univers à
tout moment du temps
passé ou futur.''
Laplace a écrit: ``.... En vertu du déterminisme universel,
l'intelligence qui connaîtrait avec une absolue précision la position
et la vitesse de tout objet dans la position initiale pourrait
calculer l'évolution de l'univers à
tout moment du temps
passé ou futur.''
Des physiciens (dont Laplace) étaient convaincus que:
``lois physiques déterministes'' 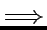 ''évènements
prévisibles.''
''évènements
prévisibles.''
``Réversibilité des lois physiques'' 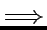 ''réversibilité
des phénomènes physiques''
''réversibilité
des phénomènes physiques''
- Paradoxalement, si on observe autour de nous: la plupart des
phénomènes
macroscopiques sont complexes, imprévisibles et irréversibles.
d'après le Dictionnaire,
``chaos'' = ``confusion'',
``désordre'', ``imprévisibilité''
peut il y avoir du ``chaos déterministe''?, c'est à dire trajectoire
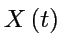 "chaotique" bien qu'elle soit déterminée par
"chaotique" bien qu'elle soit déterminée par 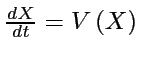 ?
?
- non,
si l'espace des états
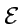 est de
dimension
2.
est de
dimension
2.
car une trajectoire forme une barrière pour les autres. (Théorème
de Poincaré-Bendixson sur les champs de
vecteurs en 2 dimensions:
l'ensemble limite est soit un point fixe, soit une orbite fermée.).
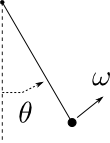
Exemple: pendule
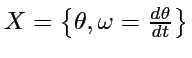
- oui:
si dim
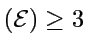 , il y
a du chaos en général (Poincaré fin XIXe,
Birkhoff 50', Arnold
60', Smale 60'...)
, il y
a du chaos en général (Poincaré fin XIXe,
Birkhoff 50', Arnold
60', Smale 60'...)
- Exemple: bille dans un billard
parfait. dim
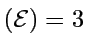 :
:
- Une trajectoire individuelle semble aléatoire, imprévisible
mais est réversible en principe.
- Une distribution (ens. de billes) se
disperse très vite et
évolue vers la distribution d'équilibre
uniforme sur
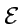 .
Cela est ``prévisible'' mais ``irréversible''
(si on oublie les états individuels).
.
Cela est ``prévisible'' mais ``irréversible''
(si on oublie les états individuels).
On parle de ``propriété de mélange'' et de
``sensibilité
aux conditions initiales''. (voir + loin).
- Remarque: ce ``mélange''
correspond à l'hypothèse
de l'ens. microcanonique en phys. statistique,
à l'origine
des lois de la thermodynamique (Maxwell, Boltzman, fin XIXe) . Les
billes indépendantes du billard ci-dessus, sont un modèle de ``gaz
parfait''.
- Comment expliquer en termes précis
ces aspects chaotiques?
Cette propriété de mélange et l'irréversibilité?
- Description du régime transitoire?
pour simplifier la description des trajectoires dans un billard, on
considère les impacts sur le bord.
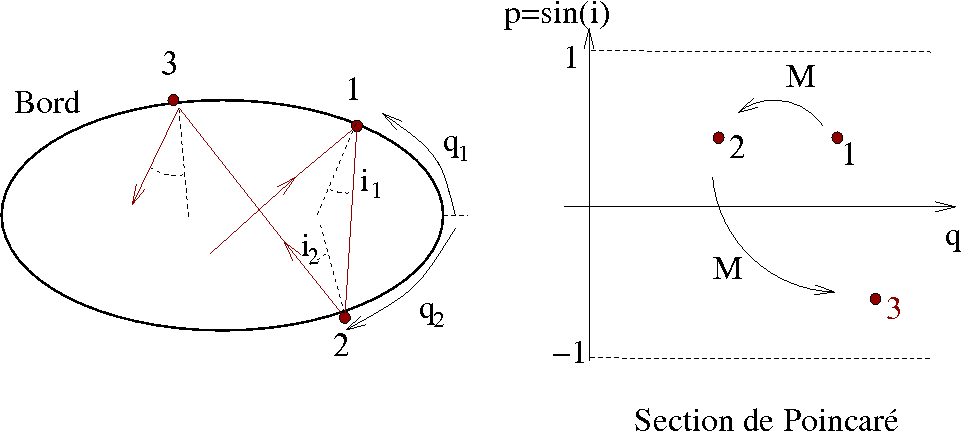
Une trajectoire devient une série
(déterministe)
C'est comme une coupe de dimension 2, transverse aux trajectoires dans
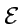 qui
est de dim. 3.
qui
est de dim. 3.
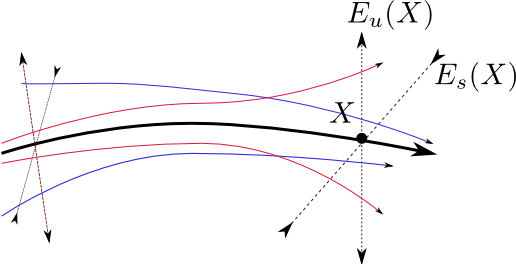
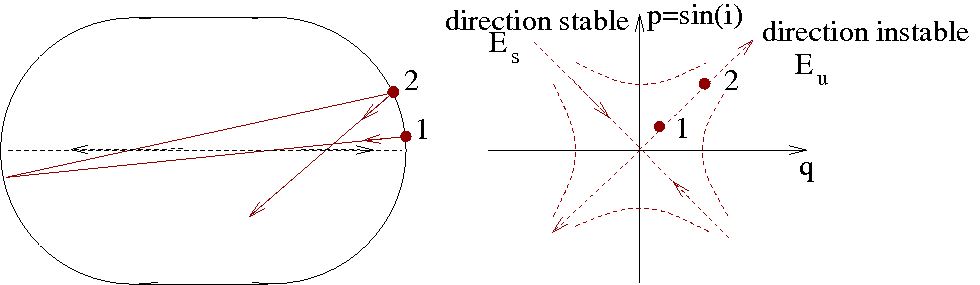
Observons une trajectoire et ses trajectoires voisines.
Le linéarisé en 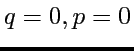 est une matrice hyperbolique
est une matrice hyperbolique
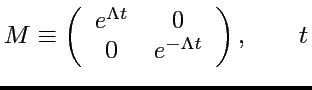
:temps entre 2
impacts
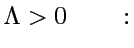
coef. d'expansion de
Lyapounov
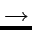 Les trajectoires voisines s'écartent comme
Les trajectoires voisines s'écartent comme
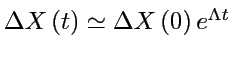 .
On dit que la trajectoire a une instabilité
hyperbolique.
.
On dit que la trajectoire a une instabilité
hyperbolique.
Un champ de Vecteur est uniformément hyperbolique
(ou
Anosov) si en tout point 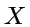 ,
il existe des directions stables
,
il existe des directions stables 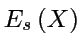 et instables
et instables 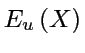 pour les trajectoires voisines
et que le taux d'expansion est strictement positif:
pour les trajectoires voisines
et que le taux d'expansion est strictement positif:
Un champ de vecteur Anosov reste Anosov si il est perturbé.
Le billard ci-dessus n'est pas unift hyperbolique, mais ``presque''
(il semble y avoir une grande
région de trajectoires hyperboliques
mais on ne sait pas démontrer si elles ne sont pas exceptionnelles).
Exemple de dynamiques unift hyperboliques:
Frederic Faure, UJF Grenoble
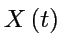 est déterminé par l'état présent
du système
est déterminé par l'état présent
du système 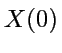 , (position et
vitesse de toutes les particules), sans hasard,
par une formule simple:
, (position et
vitesse de toutes les particules), sans hasard,
par une formule simple:
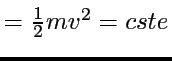 ), donc l'état est caractérisé
par 3 variables
), donc l'état est caractérisé
par 3 variables
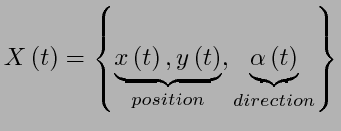 .
. ![\includegraphics[scale=0.9]{billard_schema}](img11.png)
![\includegraphics[scale=0.9]{loi_reflexion}](img12.png)
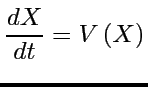
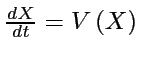
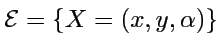

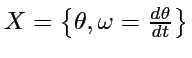
![\includegraphics[scale=1.2]{espace_phase_dim2}](img22.png)
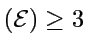
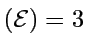

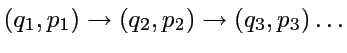
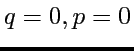
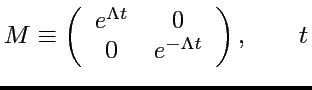 :temps entre 2
impacts
:temps entre 2
impacts