Produit extérieur.

  On pose:

Par exemple, dans le sytème de coordonnées (x¹,..,xⁿ), si et 0 sinon, si et 0 sinon. Donc

est non nul si ou (2,1) et vaut respectivement 1 et -1. On a donc bien

car deux tenseurs qui ont même composantes dans un système de coordonnées sont forcément égaux.

Propriétés du produit extérieur:

 

Preuve:

On effectue le changement d'indice de sommation:

d'où:

Comme

on a bien

 

Preuve:

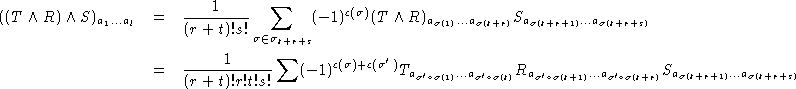
où la somme porte sur . Comme S est antisymétrique:

Avec et , on construit une permutation de qui fixe et . Donc:

où la somme porte sur . On change d'indice de sommation en remplaçant par , et on s'aperçoit que la somme obtenue ne dépend pas de : lorsqu'on somme sur , il apparaît le nombre de permutations qui fixent et , c'est-à-dire s! (r+t)!. Il vient finalement:

 

On montre la même formule pour en utilisant le calcul précédent et les propriétés de symétrie de , on conclut ainsi à l'associativité.

On généralise sans difficultés la formule (9) a un produit extérieur de n formes différentielles de degré quelconque. Par exemple, si (x₁,...,x_n) est un système de coordonnées locales, on a:

le résultat est nul si deux au moins des indices i_k sont égaux ou si les ensembles et sont distincts et vaut dans le cas contraire, ( désignant la permutation telle que ).

Base des l-formes différentielles. En coordonnées locales, on peut prendre les

(ici les i_k sont des indices permettant de différencier des formes différentielles, ce ne sont pas des composantes d'un tenseur).