


suivant: Approximation polynomiale
monter: Factorisation des polynômes
précédent: Factorisation dans
Index
Factorisation exacte
Soit P un polynôme à coefficients entiers. Lorsqu'on demande
à un logiciel de calcul formel de factoriser P, par défaut
il ne calcule pas les racines complexes approchées, mais renvoie
une factorisation exacte, sous forme de produit de facteurs
à coefficients entiers. Les degrés des facteurs peuvent
être plus grand que 2. Par exemple x4 + x + 1 ne peut pas
être factorisé en produit de polynômes à coefficients entiers
(bien qu'il ait 2 facteurs de degré 2 dans
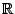 et 4 de degré 1
dans
et 4 de degré 1
dans
 ).
).
Commencons par une méthode simple de calcul des racines rationnelles
de P (les racines rationnelles correspondent à des facteurs entiers de
degré 1 de la forme qX - p de P).
Soit x = p/q une
racine rationnelle écrite sous forme de fraction
irréductible de
P = anXn + ... + a0, on a alors
0 =
P(

) =
an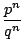
+
an-1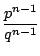
+ ... +
a0 =
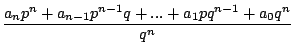
p(anpn-1 + an-1pn-1q + ... + a1qn-1) = - a0qn
et p divise donc a0qn. Comme p/q est irréductible,
cela entraine que p divise a0. De même q divise an.
Il suffit donc de tester quelles sont les racines de P parmi
toutes les fractions irréductibles
de la forme un diviseur de a0 sur un diviseur de an (attention
à ne pas oublier les diviseurs négatifs!).
Exemple: racines rationnelles de
2x2 + 3x + 1 = 0. On a p divise 1
donc vaut 1 ou -1, q divise 2 donc vaut 1 ou 2. On teste
donc 1, -1, 1/2, -1/2. On obtient ici la factorisation complète
du polynome (les racines sont -1 et -1/2)
2x2 + 3x + 1 = 2(x + 1)(x + 1/2)
Remarques :
- Pour un polynome aléatoire, on ne trouvera aucune racine
rationnelle.
- Cette méthode n'est pas très efficace, car factoriser
un entier peut être long, le nombre de tests peut être très
grand (si an et a0 ont beaucoup de facteurs), les logiciels
de calcul formel utilisent des méthodes appelées p-adiques pour trouver
les racines rationnelles d'un polynome (on calcule d'abord les racines
de P modulo p puis modulo pk pour k assez grand).
On pourrait aussi penser à calculer les racines complexes approchées
et voir si en multipliant par an on est proche d'un entier,
on testerait alors le rationnel correspondant.
Pour déterminer les facteurs à coefficients entiers de plus
grand degré, il n'existe pas de méthode aussi simple.
On peut calculer des valeurs approchées des racines complexes
et essayer de créer des paquets de racines complexes, puis tester
si
an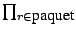 (X - r) est à coefficients entier
(aux erreurs d'arrondi près). Par exemple si on calcule les
racines complexes approchées de
x6 +2x3 - x2 + 1, on pourra composer
un facteur de degré 3 à coefficients entiers en rassemblant
les racines de x3 + x + 1.
Les logiciels de calcul formel utilisent des algorithmes modulaires
et p-adiques (consistant à factoriser le polynome modulo p).
(X - r) est à coefficients entier
(aux erreurs d'arrondi près). Par exemple si on calcule les
racines complexes approchées de
x6 +2x3 - x2 + 1, on pourra composer
un facteur de degré 3 à coefficients entiers en rassemblant
les racines de x3 + x + 1.
Les logiciels de calcul formel utilisent des algorithmes modulaires
et p-adiques (consistant à factoriser le polynome modulo p).



suivant: Approximation polynomiale
monter: Factorisation des polynômes
précédent: Factorisation dans
Index
Retour à la page principale de mat249
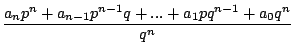
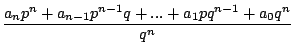
![]() (X - r) est à coefficients entier
(aux erreurs d'arrondi près). Par exemple si on calcule les
racines complexes approchées de
x6 +2x3 - x2 + 1, on pourra composer
un facteur de degré 3 à coefficients entiers en rassemblant
les racines de x3 + x + 1.
Les logiciels de calcul formel utilisent des algorithmes modulaires
et p-adiques (consistant à factoriser le polynome modulo p).
(X - r) est à coefficients entier
(aux erreurs d'arrondi près). Par exemple si on calcule les
racines complexes approchées de
x6 +2x3 - x2 + 1, on pourra composer
un facteur de degré 3 à coefficients entiers en rassemblant
les racines de x3 + x + 1.
Les logiciels de calcul formel utilisent des algorithmes modulaires
et p-adiques (consistant à factoriser le polynome modulo p).