

Chapitre 1 Pour s’amuser en arithmétique
1.1 Calcul de 555555562−444444452
Calculer
555555562−444444452 et plus généralement calculer
(5...56)2−(4...45)2 pour des nombres ayant p chiffres.
On calcule avec Xcas :
62−52=11 (l’écriture décimale comporte 2 fois le chiffre un),
562−452=1111 (l’écriture décimale comporte 4 fois le chiffre un),
....
555555562−444444452=1111111111111111 (l’écriture décimale comporte 16
fois le chiffre un).
Il semble donc que l’on a à démontrer que :
(5...56)2−(4...45)2 pour des nombres ayant p chiffres vaut un nombre dont
l’écriture décimale comporte 2p fois le chiffre un.
Pour le démontrer, on va simplement d’utiliser l’identité remarquable :
a2−b2=(a−b)(a+b)
On a (p=8) :
555555562−444444452=(55555556+44444445)(55555556−44444445)=100000001*11111111=1111111111111111.
Plus généralement, si on pose xp le nombre qui s’écrit avec p fois
le chiffre 1,
on doit calculer :
(5*xp+1)2−(4*xp+1)2=(9*xp+2)(xp).
On a xp=11...1=10p−1+...10+1=10p−1/9 donc :
9xp+2=10p+1 et
(9xp+2)(xp)=10pxp+xp=102p−10p/9+10p−1/9=102p−1/9=x2p
Ou plus simplement :
10pxp s’écrit avec p fois le chiffre 1 suivi de p fois le
chiffre 0, donc 10pxp+xp s’écrit avec 2p fois le chiffre 1.
1.1.1 Trouver un exemple du même type
On remarque que pour obtenir le même résultat il suffit que :
a=k*xp+1 et b=h*xp+1 avec 0 ≤ h<k ≤ 9.
On a a−b=(k−h)xp, il faut donc faire en sorte que
a+b=10p+1
On a a+b=(h+k)xp+2 c’est à dire prendre h+k=9 avec k>h.
Si k=8 et h=1 on a 888888892−111111122=7777777777777777
Si k=7 et h=2 on a 777777782−222222232=5555555555555555
Si k=6 et h=3 on a 666666672−333333342=3333333333333333
Si k=5 et h=4 on a l’exemple traité.
1.2 Si b=11115555 alors b+1 est un carré
1.2.1 Vérification avec Xcas
On tape :
sqrt(11115556)
On trouve :
3334
On vérifie :
33342=11115556
1.2.2 Généralisation
On remarque que :
15+1=42
1155+1=342
Soit b=11...155...5 dont l’écriture contient p fois le chiffre 1 et p
fois le chiffre 5.
On a donc :
si x s’écrit avec p fois le chiffre 1, on a x=11...1=10p−1+...10+1=10p−1/9,
b=x*10p+5x=x(10p+5)=(10p−1)(10p+5)/9=(102p+4*10p−5)/9
Remarque : Pour ne pas alourdir les notations on ne met pas d’indice à x ni à b.
On en déduit que :
b+1=(102p+4*10p+4)/9=(10p+2/3)2
On a :
10p+2/3=3(10p−1/9)+1=3x+1
Ou encore :
puisque 10p=9x+1, on a b+1= x*10p+5x+1=9x2+x+5x+1=(3x+1)2
Conclusion :
b+1=11...155...5+1 est le carré de 33...3+1 dont l’écriture contient
p fois le chiffre 3.
1.2.3 Trouver un exemple du même type
On peut faire des essais avec b ayant deux chiffres puis, avec b
ayant quatre chiffres : quand b+1 est-il un carré ?
Ou bien :
On suppose que b=m*x*10p+n*x (0<m<10 et 0 ≤ n<10) et on cherche m et n pour que b+1
soit un carré.
On a 10p=9x+1 donc b+1=9m*x2+m*x+n*x+1=(3*k*x+1)2
On choisit pour m un carré (m=k2) : m=1 ou m=4 ou m=9.
Si m=1 on doit avoir (m+n=2*3*k) m+n=6 et on retrouve l’exemple traité.
Si m=4 on doit avoir (m+n=2*3*k) m+n=12 et on trouve n=8, l’exemple
cherché est donc :
44...488...8+1 est le carré de 66..6+1
Si m=9 on doit avoir m+n=2*3*3=18 et on trouve n=9 l’exemple cherché
est donc :
99...9 dont l’écriture contient 2p fois le chiffre 9 est un carré. Cela
on le savait!!! puisque 99...9+1=102p=(10p)2
1.3 495 et 6174
Étant donné un nombre n de s chiffres au plus non tous égaux, on
définit le nombre nA obtenu en
rangeant les chiffres de n dans l’ordre croissant et le nombre nD obtenu en
rangeant les s chiffres de n dans l’ordre décroissant en rajoutant des
zéros pour que nD ait s chiffres (si n=21, nA=12 et nD=2100).
Soit f la fonction qui a n fait correspondre nD−nA.
On veut étudier les points fixes de f pour s=3 et pour s=4.
On va montrer que pour s=3, f a un point fixe qui est égal à 495 et
que pour tout n, f@6(n)=495 (f@@6(n) désigne f(f(f(f(f(f(n))))))).
On va montrer que pour s=4, f a un point fixe qui est égal à 6174 et
que pour tout n, f@7(n)=6174 (f@@7(n) désigne f(f(f(f(f(f(f(n)))))))).
On va montrer cela à l’aide d’un programme qui va tester tous les nombres
n de 3 (resp 4) chiffres au plus, non tous égaux :
ce programme suppose que le résultat est vrai car sinon le programme ne
s’arrête pas!!!!
On remarque que :
f(495)=954-459=495
f(6174)=7641-1467=6174
1.3.1 Les chiffres d’un nombre
La procédure chiffres0 renvoie un couple composé de la liste des
chiffres du nombre et du nombre de chiffres.
chiffres0(n):={
local s,ch;
ch:=string(n);
s:=size(ch);
return (asc(ch)-[seq(48,s)],s);
}
On tape :
chiffres0(6174)
On obtient :
[6,1,7,4],4
On fait la procédure nombre qui reconstitue le nombre à partir de la
liste de ces chiffres. Il ne faut pas que la chaine commence par zéro car
sinon expr considère que la chaine est une écriture en base 8 (par
exemple expr("016")=14 car en base 8, 14 s’écrit "16").
nombre(ch):={
local s,j,chaine;
s:=size(ch);
chaine:=char(ch+[seq(48,s)]);
tantque (chaine[j]==0)faire j:=j+1; ftantque;
chaine:=mid(chaine,j);
return expr(chaine);
}
On peut aussi utiliser la commande horner de Xcas qui donne la
valeur en un point d’un polynôme définit par la liste de ses coefficients
par puissances décroissantes.
Ainsi horner([6,1,7,4],10)=6174
1.3.2 La fonction f
On écrit la fonction etape0 qui a 2 arguments le nombre n et le
nombre de chiffres autorisés s : ainsi f(n)=etape0(n,4)
etape0(n,s):={
local ch,chA,chD,t,nA,nD;
si (n==0) return n;fsi;
ch,t:=chiffres0(n);
chA:=SortA(ch);
chD:=SortD(ch);
nA:=nombre(chA);
nD:=nombre(chD)*10^(s-t);
return nD-nA;
};
En utilisant la fonction horner de Xcas au lieu de nombre,
on écrit la fonction etape (f(n)=etape(n,4)) puis, on écrit la
fonction test pour tester un nombre quelconque en itérant la fonction
f :
chiffres(n):={
local ch,t;
ch:=string(n);
t:=size(ch);
return (asc(ch)-[seq(48,t)],t);
};
etape(n,s):={
local ch,chA,chD,t,nA,nD;
(ch,t):=chiffres(n);
chA:=SortA(ch);
chD:=SortD(ch);
nA:=horner(chA,10);
nD:=horner(chD,10)*10^(s-t);
return nD-nA;
};
test(n,s):={
si (n==0) "0 non permis";fsi;
si (n>10^s) alors return s+" chiffres au plus";fsi;
si (irem(n,horner([seq(1,s)],10))==0) alors
return s+" chiffres non identiques"
fsi;
si (s==3) alors
tantque (n!=495) faire print(n);n:=etape(n,s);ftantque;
fsi;
si (s==4) alors
tantque (n!=6174) faire print(n);n:=etape(n,s);ftantque;
fsi;
return n;
};
On écrit une première "démonstration" en testant tous les nombres en
ordonnant leur chiffres pour ne pas faire 103 (resp 104) tests : c’est le
fait que le programme s’arrête qui prouvera que 495 (resp 6174) est un point
fixe de f.
On compte le nombre m d’itérations que l’on doit faire avant d’obtenir
495 (resp 6174).
Pour 495 :
demo495():={
local j,k,l,u,n,p,m,n0;
p:=0
for (j:=0;j<10;j++){
for (k:=j;k<10;k++){
for (l:=k;l<10;l++){
if (l!=j){
n:=horner([j,k,l],10);
p:=p+1;m:=0;n0:=n;
tantque (n!=495) faire m:=m+1;n:=etape(n,3);ftantque;
print(n0,m);
}
}
}
}
return p;
}
Pour 6174
demo6174():={
local j,k,l,u,n,p,m,n0;
p:=0
for (j:=0;j<10;j++){
for (k:=j;k<10;k++){
for (l:=k;l<10;l++){
for (u:=l;u<10;u++){
if (u!=j){
n:=horner([j,k,l,u],10);
p:=p+1;m:=0;n0:=n;
tantque (n!=6174) faire m:=m+1;n:=etape(n,4);ftantque;
print(n0,m);
}
}
}
}
}
return p;
}
On trouve que pour s=3, on a tester p=210 nombres et pour tous ces
nombres le nombre d’itérations est inférieur ou égal à 6.
On trouve que pour s=4, on a tester p=705 nombres et pour tous ces
nombres le nombre d’itérations est inférieur ou égal à 7.
On peut par exemple retrouver le nombre p=705 en comptant :
Les nombres qui ont 4 chiffres différents :
il y en a comb(10,4)=210 (choix de 4 éléments parmi 10),
Les nombres qui ont 2 chiffres égaux et 2 chiffres différents :
il y en a comb(3,1)*comb(10,3)=360 (choix de 3 éléments parmi 10 et
choix de 1 parmi 3 pour savoir le chiffre qui sera répété),
Les nombres qui ont 2 fois 2 chiffres égaux :
il y en a comb(10,2)=45 (choix de 2 éléments parmi 10),
Les nombres qui ont 3 chiffres égaux :
il y en a comb(2,1)3*comb(10,2)=90 (choix de 2 éléments parmi 10 et
choix de 1 parmi 2 pour savoir le chiffre qui sera répété),
Donc en tout : 210+360+45+90=705
On remarque que :
-
si s=3, nD=a*102+b*10+c avec a≥ b≥ c et
a>c on a nA=c*102+b*10+a et
nD−nA=(a−c)*(102−1) ou encore
nD−nA=9*(a−c)*11 avec 10>a−c>0
On peut donc faire une démonstration plus rapide puisqu’il suffit de
regarder 9 nombres au lieu de 210. Les nombres de la forme k*(102−1)
s’écrivent si k+k1=10, [k00]−[k]=[(k−1)9k1], il suffit donc de tester
les 5 nombres :
099,198,297,396,495. - si s=4, nD=a*103+b*102+c*10+d avec a≥ b≥ c≥ d et
a>d on a nA=d*103+c*102+b*10+a et
nD−nA=(a−d)*(103−1)+(b−c)*102−10 ou encore
nD−nA=9*((a−d)*111+(b−c)*10) avec 10>a−d>0 et 10>b−c ≥ 0.
On peut donc faire une démonstration plus rapide puisqu’il suffit de
regarder 90 nombres au lieu de 705.
On écrit :
demorapide():={
local j,k,n,p,m,n0;
for (j:=1;j<10;j++){
for (k:=0;k<10;k++){
n:=9*(j*111+k*10)
m:=0;n0:=n;
tantque (n!=6174) faire m:=m+1;n:=etape(n,4);ftantque;
print(n0,m);
}
}
return "fin";
}
On cherche la liste des nombres à tester :
atester():={
local j,k,n,ch,nA,chA,l;
l:=[];
for (j:=1;j<10;j++){
for (k:=0;k<10;k++){
n:=9*(j*111+k*10);
ch:=chiffres(n)[0];
chA:=SortA(ch);
nA:=horner(chA,10);
if (member(nA,l)==0) {l:=append(l,nA);}
}
}
return sort(l);
}
On obtient une liste de 30 éléments :
[189,288,378,468,558,999,1179,1269,1278,1359,1377,1449,
1467,1557,1899,2268,2358,2367,2448,2466,2556,2799,3357,
3447,3456,3555,3699,4446,4455,4599]
On teste les nombres de cette liste dans demorapide2 :
demorapide2():={
local l,s,n,n0,m,j;
l:=atester();
s:=size(l);
for (j:=0;j<s;j++){
n:=l[j];
n0:=n;
m:=0;
tantque (n!=6174) faire m:=m+1;n:=etape(n,4);ftantque;
print(n0,m);
}
return "fin";
}
On trouve par exemple que pour 9351=9*(9*111+4*10) il faut 6 itérations.
Mais comme f(9730)=9730-379=9351, pour 9730 il faut 7 itérations.
1.3.3 Un peu de mathématiques
Comment sécrivent, en base 10, les nombres de la forme 9*(a*111+b*10)
où a et b sont des entiers entre 0 et 9 avec 0<a.
On a (si on écrit le nombre 100*a+b*10+c de chiffres a,b,c
sous la forme [abc]) :
9*(a*111+b*10)=(10-1)*(a*111+b*10)=
[aaa0-(aa0+a)+b00-b0]=[ab00-ba]=
si b>0 [a(b-1)b1a1] avec a+a1=10 et b+b1=9 (cela fait
25 nombres à traiter).
si b=0 [(a-1)99a1] avec a+a1=10 (cela fait 5 nombres à
traiter).
Les couples aa1 et (b-1)b1 sont donc :
55 46 37 28 19 et 44 35 26 17 08
Les nombres à traiter sont donc :
5544 5535 5526 5517 5508 4644 4635 4626 4617 4608 3744 3735 3726
3717 3708 2844 2835 2826 2817 2808 1944 1935 1926 1917 1908
et
999 1899 2799 3699 4599
On retrouve la liste obtenue précédemment :
[189,288,378,468,558,999,1179,1269,1278,1359,1377,1449,
1467,1557,1899,2268,2358,2367,2448,2466,2556,2799,3357,
3447,3456,3555,3699,4446,4455,4599]
1.3.4 Prolongements
On peut regarder ce qui se passe pour s=2, s=5 etc ...
Par exemple pour s=2 les itérés de 12 sont :
9,81,63,27,45,9.... il n’y a donc pas de point fixe.
On trouve par exemple que les itérés de 02345 sont :
51975,81972,85932,74943 et 74943 est un point
fixe et
que les itérés de 12345 sont 41976... et 41976 est aussi un
point fixe.
que les itérés 31777 sont 63954... et on trouve un autre
point fixe 63954
Il y a donc plusieurs points fixes. Il faut trouver ces points fixes et aussi
savoir si les itérés aboutissent toujours a un point fixe ou si il existe des cycles.
Les points fixes trouvés s’écrivent [ab9(8−b)(10−a)], testons alors des
nombres de cette formes :
31977 : on trouve un autre point fixe 83952
32967 : on trouve un autre point fixe 73953
12969 : on trouve un autre point fixe 86922
A vous de jouer !!!!
1.4 La suite 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5,....
On considère la suite u définie par :
u0=1 (un 1), u1=u2=2 (deux 2), u3=u4=u5=3 (trois 3) etc...
Quel est la valeur de u2010 ?
1.4.1 La correction avec un programme Xcas
Attention !!! en Xcas les indices commencent à 0.
On peut écrire un programme qui renvoie la liste des p+1 premiers termes de
cette suite et qui donne la valeur du dernier terme qui est d’indice p.
On tape :
valeurL(p):={
local j,n,L;
j:=0;
n:=1;
L:=[1];
tantque j<p faire
n:=n+1;
j:=j+n;
L:=append(L,n$n);
ftantque;
L:=mid(L,0,p+1);
retourne L,n;
}
:;
On tape :
valeurL(2010)[1]
On obtient :
63
1.4.2 La correction mathématique avec Xcas
On a :
-
1 a pour indice 0=1-1
- 2 a pour indice 1 et 2=1+1
- 3 a pour indice 3=1+2, 4 et 5=1+2+(3-1)
- 4 a pour indice 6=1+2+3, 7, 8 et 9=1+2+3+(4-1)
- ....
- p a pour indice 1+2+...+p−1=p(p−1)/2,... p(p−1)/2+p−1=p(p+1)/2−1 ou
encore si 1+2+...+p−1=p(p−1)/2 ≤ k<p(p−1)/2+p−1=p(p+1)/2 alors uk=p
On cherche p=u2010 c’est à dire on cherche p vérifiant :
p(p−1)/2≤ 2010< p(p+1)/2 ou encore
p(p−1)≤ 4020< p(p+1) ou encore
p2−p−4020 ≤ 0 et p2+p−4020 > 0 et p>0
Donc p est entre les racines de x2−x−4020 est est supérieur à la plus
grande racine de x2+x−4020 c’est à dire :
−1/2+√1+4*4020/2<p ≤ 1/2+√1+4*4020/2<p+1 c’est à dire
p est la partie entière de 1/2+√1+4*4020/2=1/2+√1/4+4020.
On peut donc utiliser la fonction round, on a round(a)=floor(a+0.5)
et donc k=round(sqrt(2*p+0.25)).
On peut remarquer que :
k(k−1)=(k−1/2)2−1/4
k(k+1)=(k+1/2)2−1/4
On cherche k tel que : k(k−1)=(k−1/2)2−1/4 ≤ 2p<(k+1/2)2−1/4=k(k+1)
c’est à dire (k−1/2)2≤ 2p+1/4<(k+1/2)2
donc k=round(sqrt(2*p+0.25))
On tape :
valeur(p):={
local k;
k:=round(sqrt(2*p+0.25));
retourne k;
}
:;
On tape :
valeur(2010)
On obtient :
63
On tape :
valeur(63*31)
On obtient :
63
On tape :
valeur(63*32-1)
On obtient :
63
On tape :
valeur(63*32)
On obtient :
64
car 63*62/2=63*31=1953<2010<63*32−1=2015=63*62/2+63−1.
Les 63 termes d’indices 1953,1954,....2015 valent donc 63.
1.5 7 a un multiple qui ne s’écrit qu’avec des 1
1.5.1 Essais avec Xcas
On tape :
irem(1,7) réponse 1
irem(11,7) réponse 4
irem(111,7) réponse 6
irem(1111,7) réponse 5
irem(11111,7) réponse 2
irem(111111,7) réponse 0
1.5.2 Observations
1/ On n’a pas obtenu 3 comme reste car :
irem(31,7)=3 et donc
irem(311...1,7)=3
2/ Pourquoi obtient-on 0 comme reste ?
notons xp=11...1=10p−1/9 le nombre s’écrivant avec p fois le
chiffre 1. On veut montrer qu’il existe p tel que xp est divisible par 7.
La suite des restes est périodique car les restes sont en nombres finis
et supposons que :
irem(xp,7)=irem(xq,7) avec p>q
on a alors :
irem(xp-xq,7)=0
On a xp−xq est divisible par 7 et
xp−xq=10p−10q/9=10q10p−q−1/9=10qxp−q
Donc 10qxp−q est divisible par 7, comme 10 et 7 sont premiers entre eux
on en déduit que xp−q est divisible par 7.
1.5.3 x2003 et x2004 sont-ils des multiples de 7 ?
On a x6=111111=7*15873 (iquo(111111,7)=15873 et irem(111111,7)=0)
donc x12 est divisible par 7 ainsi que x6k.
Comme 2004 est divisible par 6, x2004 est divisible par 7, par contre
2003=6k+5 donc le reste de la division de x2003 par 7 est le même que celui de la division de x5 par 7 c’est à dire ce reste est égal à 2.
1.6 Tout nombre a un multiple qui ne s’écrit qu’avec des 1 et des 0
1.6.1 Tout nombre premier avec 10 a un multiple qui ne s’écrit qu’avec des 1
Un nombre qui ne s’écrit qu’avec des 1, sera dit nombre en 1, si il s’écrit
avec p uns, on le notera xp.
On va tout d’abord montrer que tout nombre n premier avec 10 a un multiple
m qui ne s’écrit qu’avec des 1 (il existe k telque m=xp=1..1=k*n).
Si n n’est pas premier avec 10, on écrit n=2a*5b*q
(avec pgcd(q,10)=1), on multiplie ce nombre n par
2b−a si b>a ou par 5a−b si b<a pour obtenir le nombre
q*10|a−b| et on applique le résultat précédent à q et obtenir
ainsi un multiple de n qui s’écrit avec des 1 suivi par |a−b| zéros.
Exemple :
si n=37 on a 37*3=111
si n=74=2*37 on a 74*3*5=74*15=1110
si n=185=5*37 on a 185*3*2=185*6=1110
1.6.2 Des remarques
Un nombre qui ne s’écrit qu’avec des 1 sera dit nombre en 1, si il
s’écrit avec p uns, on le notera xp et on a donc :
xp=(10p−1)/9=iquo(10p−1),9).
Si un nombre premier avec 10 est le diviseur d’un nombre en 1, il divise une
infinité de nombre en 1. En effet
x2p.... xkp sont des multiple de xp car on a x2p=xp*(10p+1)
et xkp=xp*(10(k−1)p+...+10p+1).
On a x2=11, x3=111=3*37, x4=11*101, x5=11111=41*271....
Existe-t-il des nombres en 1 qui soit premiers ?
Oui! il y x19 et x23.
On tape :
isprime(iquo(10^19-1,9)) et on obtient true
on tape :
isprime(iquo(10^23-1,9)) et on obtient true
Existe-t-il une infinité de nombres en 1 qui soit premiers ?
On ne sait pas !
Étant donné un nombre premier a, on va essayer, dans la suite, de trouver
le plus petit p pour que a soit un diviseur de xp.
Si a=3, on a p=3
Si a=37, on a p=3 et 3 est un diviseur de 37-1
Si a=7, on a p=6 et 6 est un diviseur de 7-1
1.6.3 La suite des restes de 111...1 par n
Pour avoir la suite des restes, on écrit, avec Xcas, le programme
suivant :
resteun(n):={
local r,q,a,b;
a:=0;
b:=0;
while (irem(n,2)==0) {
n:=iquo(n,2);
a:=a+1;
}
while (irem(n,5)==0) {
n:=iquo(n,5);
b:=b+1;
}
r:=1;print(r);
q:=0;
while (r!=0){
r:=10*r+1;
q:=10*q+iquo(r,n);
r:=irem(r,n);
print(r);
}
if (a>b) q:=q*5^(a-b); else q:=q*2^(b-a);
return(q);
};
Ce programme suppose que le résultat est vrai car sinon le programme ne
s’arrête pas!!!!
Le fait de faire afficher les restes de la division de
1, 11, 111,... par n montre déjà que la suite des restes est
périodique puisque ces restes sont en nombre fini car ils
sont positifs ou nuls et inférieurs à n. Mais pourquoi la suite des
restes contient-elle toujours 0 ?
Supposons que (10k−1)/9 et (10l−1)/9 aient le même reste dans la
division par n (avec pgcd(n,10)=1 et k>l).
Cela veut dire que (10k−10l)/9=10l*(10k−l−1)/9 est divisible par n
donc que (10k−l−1)/9 est divisible par n (n divise
10l*(10k−l−1)/9 n est premier avec 10l donc n divise
(10k−l−1)/9, ce qui prouve bien que la suite des restes contient 0 (le nombre formé par k−l 1 est divisible par n).
1.6.4 Relation entre n et p le nombre de 1 de xp=111...1 où
xp est un multiple de n
On cherche la fonction R de n qui détermine p, où p est le plus
petit entier tel que xp=11...1=10p−1/9 soit un multiple de n.
Ce qui veut dire que 10p−1/9=0 mod n
Quelques essais
Tout d’abord quelques essais :
x2=11 est divisible par 11 (R(11)=2)
x22 est divisible par 112 (R(112)=22=2*11)
x3=111 est divisible par 3 et par 37 (R(3)=3 et R(37)=3))
x9=111111111 est divisible par 9
x27 est divisible par 27=33 (R(33)=33 car x27=111111111(1018+109+1) et 1018+109+1 est divisible par 3)
x6 est divisible par 7 (R(7)=6)
x42 est divisible par 49=72 (R(72)=42=6*7)
x6 est divisibble par 13 (R(13)=3 car x6=3*7*11*13*37)
x6 est divisible par 21=3*7 (R(3*7)=6)
On va montrer que :
0/ si p=R(n) (xp est un multiple de n avec p le plus petit possible)
alors quelque soit k,
xk*p est encore un multiple de n, et réciproquement si
xc est un multiple de n, il existe k tel que c=k*p
1/ si n est un multiple de 3 alors xn est divisible par n (p=n)
2/ si n est premier avec 30 alors p est un diviseur de n−1
3/ si n est premier avec 10, si n=n1*n2 avec n1 et n2 premiers (n1 ≠ n2), et si xp1 est divisible par
n1 et xp2 est divisible par n2 alors si p= ppcm(p1,p2),
xp est divisible par n.
4/ si n=n1k alors si xp1 est divisible par n1 et si
p=p1*n1k−1 alors xp est divisible par n.
n est une puissance de 3
On suppose que n=3k, et on montre par récurrence sur k que
R(3k)=3k et que R(3k) n’est pas un multiple de 3k+1.
Pour k=1, on a x1=1 et x2=11 ne sont pas divisibles par 3 et x3=111
est divisible par 3 et x3 n’est pas divisible par 9.
supposons la propriété vraie pour k-1, R(3k−1)=3k−1
Posons b=R(3k−1)=3k−1 et c=R(3k).
Par hypothèse de récurrence xb est divisible par b et
xc est divisible par 3*b donc par b. Ainsi,
d’après la réciproque de la propriété 0, c est un multiple de
R(b)=b : c=q*b
En mettant xb en facteur dans xc, on a :
xc=xb(10(q−1)b+...+10b+1)
xb est divisible par 3k−1 mais pas par 3k
xc est divisible par 3k donc 10(q−1)b+...++10b+1 est divisible par
3, donc comme 10m=1 mod 3, on en déduit que q=0 mod 3,
et comme c est le plus petit possible q=3 et c=q*b=3*b.
Donc xc=xb(102*b+10b+1) est divisible par 3k mais pas par 3k+1
car 102*b+10b+1 n’est pas divisible par 3 (10m=1 mod 9 donc
102*b+10b+1=3 mod 9)
n est premier supérieur à 6
On cherche donc p tel que 10p=1 mod n.
La suite des restes possibles est n mais comme n et 9 sont premiers entre
eux, il existe u et v avec 0<v<n uniques (identité de Bézout)
tels que :
u*n−v*9=1 ou encore 10*v+1=u*n+v ce qui veut dire que le reste égal à
v n’est pas obtenu.
Parmi les n−1 restes possibles de la division d’un xk par n,
considérons la relation déquivalence sur les n entiers 0,1,...,n-1:
r1 ≃ r2 si il existe k tel que r1*10k +xk=r2+q*n.
On a alors puisque 9*xk+1=10k, r1−r2+(9*r1+1)*xk=q*n.
On a donc p éléments équivalents à 1,
Cherchons la periodicité de la suite des restes de r1*10k +xk par n,
c’est à dire le nombre l d’éléments de la classe r1.
On a r1−r1+(9*r1+1)*xl=(9*r1+1)*xl=q*n, donc n divise
(9*r1+1)*xl, n est premier avec (9*r1+1) donc n divise xl
donc l=p*l1.
Mais r1*10p+xp=r1 mod n donc l=p.
Donc si il y a c classes, il y une classe ayant un seul élément et les
autres classes ont p éléments donc n=1+p*(c−1) c’est à dire p
divise n−1.
1.6.5 Les nombres premiers qui ne s’écrivent qu’avec des 1
Comment sont-ils répartis ?
Un premier test pour trouver le premier nombre premier après 11 qui ne
s’écrit qu’avec des 1.
On tape :
testun():={
local j;
j:=111;
tantque !isprime(j) faire
j:=10*j+1;
ftantque;
retourne j;
};
On tape :
testun()
On obtient le nombre qui s’écrit avec avec 19 fois le chiffre 1:
1111111111111111111
Un deuxième test pour trouver le deuxième nombre premier après 11 qui ne
s’écrit qu’avec des 1.
On tape :
testdeux():={
local j;
j:=testun();
j:=10*j+1;
tantque !isprime(j) faire
j:=10*j+1;
ftantque;
retourne j;
}:;
On tape :
testdeux()
On obtient le nombre qui s’écrit avec avec 23 fois le chiffre 1:
11111111111111111111111
Pour avoir les n premiers, on tape :
testn(n):={
local j,k,L;
j:=111;
k:=1;
L:=11;
tantque k<n faire
si isprime(j) alors
L:=L,j;
k:=k+1;
fsi;
j:=10*j+1;
ftantque;
retourne L;
}:;
On tape :
testn(4)
On obtient une liste de 4 nombres et le dernier s’écrit avec avec 317 fois
le chiffre 1:
11111111111111111111111111111111111111111111111111111111111111111111111
11111111111111111111111111111111111111111111111111111111111111111111111
11111111111111111111111111111111111111111111111111111111111111111111111
11111111111111111111111111111111111111111111111111111111111111111111111
111111111111111111111111111111111
puis testn(5) depasse les capacités de Xcas
1.7 Le réseau des entiers
Exercice
Soient 5 points distincts appartenant au réseau des entiers et les segments
définis par ces 5 points.
Combien y-a-t-il de segments ?
Montrer que le milieu d’au moins un segment appartient aussi au réseau.
Il y a comb(5,2)=10 segments.
Les points ont des abscisses paires ou impaires et des ordonnées paires ou
impaires : cela fait 4 sortes de points. Comme on a 5 points, il y a toujours
deux points par exemple A et B qui sont de la même sorte.
Si les deux points ont comme coordonnèes :
-
A=(2n,2p) et B=(2m,2q) le milieu M de AB a comme coordonnèes :
n+m,p+q
- A=(2n,2p+1) et B=(2m,2q+1) le milieu M de AB a comme
coordonnèes :
n+m,p+q+1
- A=(2n+1,2p) et B=(2m+1,2q) le milieu M de AB a comme
coordonnèes :
n+m+1,p+q
- A=(2n+1,2p+1) et B=(2m+1,2q+1) le milieu M de AB a comme
coordonnèes :
n+m+1,p+q+1
Donc dans tous les cas M appartient au réseau.
1.8 Le quadrillage
On considère un rectangle de dimension p,q avec p et q entiers.
On munit ce rectangle d’un quadrillage à coordonnées entières.
-
Écrire une fonction qui trace un rectangle de dimension p,q, son
quadrillage et une de ses diagonales.
- On trace une diagonale de ce rectangle.
Combien de de carreaux cette diagonale traverse-t-elle ?
On traitera les exemples :
p=3,q=5, p=3,q=6,p=6,q=9,p=6,q=10,,p=6,q=11....
puis on traitera le cas général.
- Écrire une fonction nbcarreaux qui étant donné p,q renvoie
le nombre de carreaux traversés par cette diagonale.
Tracer le nuage des points (x,y=nbcarreaux(240,x)) pour
0≥ x ≥ 300. Tracer sur un autre graphique
la ligne polygonale reliant ces points.
1.8.2 La solution
-
quadrillage(p,q):={
local k,j,L:=segment(0,p+i*q);
pour j de 0 jusque p faire
L:=L,segment(j,j+i*q);
fpour;
pour k de 0 jusque q faire
L:=L,segment(i*k,p+i*k);
fpour
L;
}:;
On tape :
quadrillage(3,5)
On obtient :

- On remarque que la diagonale entre dans le premier carreau, puis elle entre
dans un nouveau carreau lorsqu’elle coupe
une ligne verticale ou une ligne horizontale ou à la fois une ligne verticale
et une ligne vhorizontale.
Puisqu’il y a p−1 verticales et q−1 horizontales à traverser,
si la diagonale ne coupe jamais à la fois une verticale et une horizontale
(c’est à dire si elle ne contient pas de points à coordonnées entières
à part le point de départ et le point d’arrivèe) le
nommbre de carreaux traversés est 1+p−1+q−1=p+q−1.
Si la diagonale coupe r fois, une verticale et une horizontale en même
temps, c’est à dire si elle contient r+2 points à coordonnées
entières (+2 en comptant le point de départ et le point d’arrivèe) le
nommbre de carreaux traversés est p+q−1−r.
Que vaut r ?
La diagonale a comme équation y=q*x/p =q1*x/p1 où p=p1*d et q=q1*d
avec d=pgcd(p,q) et elle aura des points à coordonnées entières
chaque fois que x est entier et que p1 divise q1*x. Puisque p1 et q1
sont premiers entre eux, p1 divise q1*x si x est un entier multiple de p1. Cela se produit lorsque 0≥ x≥ p,
pour x=0,x=p1,x=2*p1...x=d*p1=p, soit d+1 fois.
On a donc r+2=d+1 et le
nommbre de carreaux traversés est p+q−pgcd(p,q).
- On tape la fonction nbcarreaux :
nbcarreaux(p,q):={
local d;
d:=gcd(p,q);
return p+q-d;
}
On tape :
nuage_points([x,nbcarreaux(240,x)]$(x=0..300))
On obtient :
 On tape :
On tape :
plotlist([x,nbcarreaux(240,x)]$(x=0..300))
On obtient :

1.9 Résolution dans ℕ* de x2=y2+z2
On veut résoudre dans ℕ* : x2=y2+z2.
Par exemple on veut avoir toutes les solutions de x2=y2+z2
pour x ≤ 200 et (x,y,z)∈ ℕ3.
On peut écrire un programme qui fait un balayage, mais cela n’est pas
efficace car beaucoup trop long !
On tape :
triplet0(n):={
local j,k,s,L;
L:=NULL;
pour j de 2 jusque n faire
pour k de 1 jusque j-1 faire
s:=sqrt(j^2-k^2);
si (type(s)==DOM_INT)alors
L:=L,[j,k,s],[j,s,k];
fsi;
fpour;
fpour;
return L;
}
:;
Puis :
A:=triplet0(200):;size(A)
On obtient (Evaluation time: 2.46) :
Done, 254
Il faut donc améliorer le programme.
Cette amélioration donne lieu à l’exercice suivant :
Exercice : amélioration
-
Montrer que si (x,y,z) est une solution tous les multiples de (x,y,z)
sont aussi des solutions.
En effet :
(kx)2=k2x2=k2y2+k2z2=(ky)2+(kz)2 pour tout k ∈ ℕ*.
On va donc d’abord chercher les solutions pour lesquelles (x,y,z) sont
premiers entre eux.
- Montrer que si (x,y,z) sont premiers entre eux dans leur ensemble et
vérifient x2=y2+z2 alors (x,y) (resp (x,z) ou (y,z)) sont
premiers entre eux.
En effet :
soit un diviseur premier d de
x et de y (resp de x et de z ou de y et de z) alors d2 divise
x2−y2=z2 (resp x2−z2=y2 ou y2+z2=x2) donc d divise z (resp
d divise y ou d divise x).
- Montrer que x est impair et que y ou z est divisible par 4.
En effet :
si x est pair x2 est un multiple de 4 donc x2=0 mod4 et
si x est impair x2 est un multiple de 4 plus 1 donc x2=1 mod4.
Supposons que y et z soient impairs :
on a y2=1 mod4 et z2=1 mod4 donc y2+z2=2 mod4
donc y2+z2 ne peut pas être un carré.
Donc y ou z est pair.
- Montrer que si z est pair alors z est un multiple de 4.
En effet si y est impair et z=2 mod4 alors y2+z2=3 mod4 donc
y2+z2 ne peut pas être un carré.
- On pose pour a et b quelconques dans ℕ* (a>b) :
x=a2+b2,
y=a2−b2
z=2ab
Montrer qu’alors on a x2=y2+z2.
En effet :
x2=a4+2a2b2+b4=a4−2a2b2+b4+4a2b2=y2+z2
donc (x,y,z) est une solution dans ℕ* de x2−y2=z2 .
- Montrer que toutes les solutions de x2=y2+z2 avec des nombres
entiers premiers entre eux dans leur ensemble sont de cette forme.
Soit x,y,z une solution de x2=y2+z2 où x,y,z sont des
nombres entiers premiers entre eux dans leur ensemble. On a montrer que y ou
z était un multiple de 4. Supposons que ce soit z.
On a :
(z/2)2=(x+y/2)(x−y/2) et
puisque x,y,z sont des nombres entiers premiers entre eux dans leur ensemble
x et y sont impairs et premiers entre eux.
Donc x+y/2 et x−y/2 sont des
nombres entiers qui sont premiers entre eux et comme leur produit est un
carré, ils sont eux aussi des carrés.
On pose a2=x+y/2 et b2=x−y/2
et on a :
x=a2+b2
y=a2−b2
z=2*a*b
On tape :
triplet(n):={
local a,b,a2,b2,m,q,p,k,L;
L:=NULL;
for (a:=2;a<sqrt(n);a++) {
a2:=a^2;
for (b:=1;b<=sqrt(n-a2) and b<a ;b++) {
b2:=b^2;
m:=a2+b2;p:=a2-b2;q:=2*a*b;
if (gcd(m,p,q)==1){
for (k:=1;k<=n/m;k++) {
L:=L,[k*m,k*p,q*k],[k*m,k*q,p*k];
}
}
}
}
return L;
}:;
Puis :
A:=triplet(200):;size(A)
On obtient instantanément :
Done, 254
Dans A on a a des triplets comme [143,55,132] et [143,132,55]
qui sont en fait 11*[13,5,12], on peut donc refaire un pogramme qui
renverra les triplets [x,y,z] qui vérifient x2=y2+z2 avec y>z et
gcd(y,z)=1.
On tape pour avoir les triplets x,y,z vérifiant x2=y2+z2 avec
x=a2+b2<n :
triplets(n):={
local a,b,a2,b2,m,q,p,k,L;
L:=NULL;
for (a:=2;a<sqrt(n);a++) {
a2:=a^2;
for (b:=1;b<=sqrt(n-a2) and b<a ;b++) {
b2:=b^2;
m:=a2+b2;p:=a2-b2;q:=2*a*b;
if (gcd(m,p,q)==1){
L:=L,[m,max(p,q),min(p,q)];
}
}
}
return L;
}:;
On suppose que n est le nombre de triplets désirés.
tripletss(n):={
local a,b,a2,b2,m,q,p,k,L;
L:=NULL;
k:=0;
a:=2;
while (k<n) {
a2:=a^2;
for (b:=1;b<a and k<n;b++) {
b2:=b^2;
m:=a2+b2;p:=a2-b2;q:=2*a*b;
if (gcd(m,p,q)==1){
L:=L,[m,max(p,q),min(p,q)];
k:=k+1;
}
}
a:=a+1;
}
return L;
}:;
Trouver les solutions en nombres entiers de x2=y2+z2 avec x=y+1.
1.10 Les paires carrées
Définition
On dit que les entiers p et q est une paire carrée si il existe deux
entiers a er b tels que q+p=a2 et q−p=b2.
Par exemple (6,10) est une paire carrée car 10−6=22 et 10+6=42.
Remarque si p et q est une paire carrée alors 2q=a2+b2 et
2p=a2−b2 donc a−b est pair et
(2q)2=(2p)2+(2ab)2=a4+b4−2a2b2+4a2b2.
Donc q2=p2+(ab)2
-
Écrire un programme qui en balayant tous les nombres de 0 à n
donne les paires carrées (p,q) avec 0 ≤ p ≤ q ≤ n,
- Montrer que si (p,q) est une paire carrée alors on a :
- Montrer que quelque soit n ∈ ℕ on soit n2=1 mod4,
soit n2=0 mod4. En déduire alors que p est pair si (p,q) est une
paire carrée.
Modifier votre programme pour tenir compte de cette information.
- Montrer que a2−b2 est un multiple de 4. En déduire que
a et b ont même parité et que a−b est pair.
Écrire un programme qui à partir de b et de a=b+2n calcule les valeurs
de p et q vérifiant q=(a2+b2)/2 et p=(a2−b2)/2 et
0 ≤ p ≤ q ≤ 1000.
- Afficher les points de coordonnées (p,q)
(0 ≤ p ≤ q ≤ 1000) où (p,q) est une paire carrée.
- Trouver les équations des droites et des courbes en forme de filets
reliants certains de ces points.
-
paire_carre0(n):={
local a,b,q,p,L;
L:=NULL;
pour p de 0 jusque n faire
pour q de p jusque n faire
a:=sqrt(q+p);
b:=sqrt(q-p);
si (a==floor(a) et b==floor(b)) alors
L:=L,[p,q];
fsi
fpour
fpour
return L
}:;
ou on utilise type pour tester si a et b sont des carrés :
paire_carre1(n):={
local a,b,q,p,L;
L:=NULL;
pour p de 0 jusque n faire
pour q de p jusque n faire
a:=sqrt(q+p);
b:=sqrt(q-p);
si (type(a)==DOM_INT et type(b)==DOM_INT) alors
L:=L,[p,q];
fsi
fpour
fpour
return L
}:;
On tape :
L1:=paire_carre1(100)
On obtient (Evaluation time: 2.26) :
[0,0],[0,1],[0,4],[0,9],[0,16],[0,25],[0,36],[0,49],
[0,64],[0,81],[0,100],[2,2],[4,5],[6,10],[8,8],[8,17],
[10,26],[12,13],[12,37],[14,50],[16,20],[16,65],
[18,18],[18,82],[20,29],[24,25],[24,40],[28,53],
[30,34],[32,32],[32,68],[36,45],[36,85],[40,41],[42,58],
[48,52],[48,73],[50,50],[54,90],[56,65],[60,61],[64,80],
[70,74],[72,72],[72,97],[80,89],[84,85],[96,100],[98,98]
On tape : dim(L1)
On obtient; 49
- Si (p,q) est une paire carrée, on a :
q+p=a2 et q−p=b2
donc p=(a2−b2)/2, donc a2−b2 est pair c’est à dire
a2−b2=0 mod4, soit a2−b2=2 mod4.
- Soit n ∈ ℕ ;
si n est pair alors n2=0 mod4, en effet, si n=2k on a
n2=4k2 et
si n est impair alors n2=1 mod4 en effet :
si n=2k+1 on a n2=4k2+4k+1.
- Donc on a :
soit a2−b2=0 mod4,
soit a2−b2=1 mod4
soit a2−b2=3 mod4.
et puisque a2−b2=0 est pair, on en déduit qu a2−b2=0 mod4
on en déduit que p est pair.
On tape :
paire_carre2(n):={
local a,b,q,p,L;
L:=NULL;
pour p de 0 jusque n pas 2 faire
pour q de p jusque n faire
a:=sqrt(q+p);
b:=sqrt(q-p);
si (a==floor(a) et b==floor(b)) alors
L:=L,[p,q];
fsi
fpour
fpour
return L
}:;
On tape :
L2:=paire_carre2()
On obtient comme précédement (Evaluation time: 1.36) :
[0,0],[0,1],[0,4],[0,9],[0,16],[0,25],[0,36],[0,49],
[0,64],[0,81],[0,100],[2,2],[4,5],[6,10],[8,8],[8,17],
[10,26],[12,13],[12,37],[14,50],[16,20],[16,65],
[18,18],[18,82],[20,29],[24,25],[24,40],[28,53],
[30,34],[32,32],[32,68],[36,45],[36,85],[40,41],[42,58],
[48,52],[48,73],[50,50],[54,90],[56,65],[60,61],[64,80],
[70,74],[72,72],[72,97],[80,89],[84,85],[96,100],[98,98]
On tape : dim(L2)
On obtient; 49
- On a si (p,q) est une paire carrée :
2p=a2−b2 donc a2−b2 est un multiple de 2 donc
a2 et b2 ont même parité donc
a et b ont même parité et donc a−b est un multiple de 2 c’est à
dire a−b est pair.
On pose :
a=b+2r
donc a2=b2+4rb+4r2 et on a :
p=(a2−b2)/2=2rb+2r2 et
q=(a2+b2)/2=b2+2rb+2r2=b2+p.
On veut obtenir toutes les paires carrées (p,q) vérifiant
0 ≥ p ≥ q ≥ n, donc on doit avoir :
0≥ b2 ≥ n i.e 0≥ b ≥ √n et
0≥ 2rb+2r2≥ n et 0≥ b2+2rb+2r2≥ n.
On tape :
supposons(b>=0 and b<=31);
simplify(solve(b^2+2*r*b+2*r^2<1000,r))
On obtient;:
[((r>((-b-sqrt(-b^2+2000))/2)) && (((-b+sqrt(-b^2+2000))/2)>r))]
On tape :
paire_carre(n):={
local b,q,p,L,r,nmax;
L:=NULL;
pour b de 0 jusque sqrt(n) faire
nmax:=(sqrt(-b^2+2*n))/2-b/2;
pour r de 0 jusque nmax faire
p:=2*r*b+2*r^2;
q:=b^2+p;
L:=L,[p,q];
fpour
fpour
return L
}:;
Puis, on tape :
L:=paire_carre(100):;
Le calcul est tres rapide !!!!!
On tape : dim(L)
On obtient instantanément : 48
On tape :
L3:=paire_carre(1000):;
Le calcul est tres rapide !!!!!
On tape : dim(L3)
On obtient : 421
- On tape : nuage_points(L3)
On obtient :
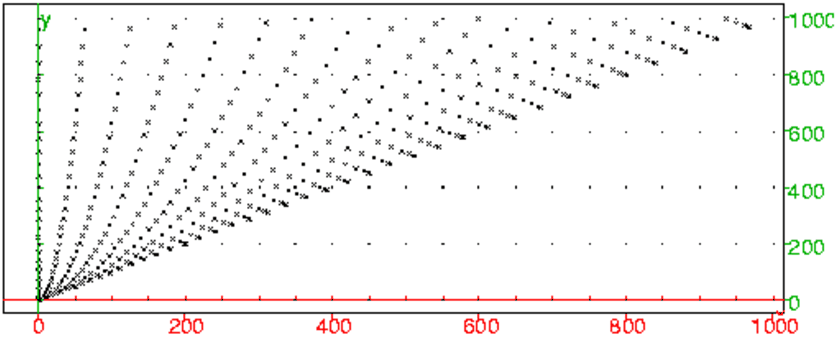
- On a q=p+b2 donc les points sont sur les droites d’équations y=x+b2 pour
b fixé.
0n a p=2nb+2n2 donc b=(p/(2n)−n) donc q=p2/(4n2)+n2
donc les points sont sur les courbes
d’équations y=x2/(4n2)+n2 pour n fixé.
On tape et on obtient :

1.11 Les triangles rectangles presque isocèles
Définition
Un triangle rectangle dont les
côtés sont :
-
les entiers a,c−1,c lorsque c est la longueur de
l’hypoténuse est un triangle rectangle presque isocèle de type 1.
- les entiers a,a+1,c lorsque c est la longueur de
l’hypoténuse est un triangle rectangle presque isocèle de type 2.
Pour trouver les triangles rectangles presque isocèles il faut et il suffit
de résoudre en nombre entiers les équations
-
a2+(c−1)2=c2, c’est à dire :
trouver les couples (a,c)∈ ℕ vérifiant a2+c2−2c+1=c2.
- a2+(a+1)2=c2,
c’est à dire :
trouver les couples (a,c)∈ ℕ vérifiant 2a2+2a+1=c2.
On veut trouver les triangles rectangles presque isocèle de type 1.
On cherche donc les couples (a,c)∈ ℕ vérifiant a2+c2−2c+1=c2 c’est
à dire :
a2=2c−1.
1.11.2 La solution de l’énoncé 1
a est donc impair i.e. a=2k+1 avec k∈ ℕ.
On a donc 4k2+4k=2(c−1) et donc c=2k2+2k+1=k2+(k+1)2
Les côtés du triangle rectangle presque isocèle de type 1 sont donc :
[2k+1,k2+(k+1)2−1,k2+(k+1)2] ou encore [2k+1,2k(k+1),k2+(k+1)2]
lorsque k ∈ ℕ.
On tape :
[2k+1,2k*(k+1),k^2+(k+1)^2]$(k=0..10)
On obtient :
[1,0,1],[3,4,5],[5,12,13],[7,24,25],[9,40,41],[11,60,61],
[13,84,85],[15,112,113],[17,144,145],[19,180,181],[21,220,221]
On peut trouver une relation de récurrence entre 2 tripletssuccessifs.
On cherche x,y,z tels que pour tout k∈ ℕ on ait :
ak=xak−1+ybk−1+zck−1.
2k+1=x*(2k−1)+y*2k*(k−1)+z*(k2+(k−1)2=2k2(z+y)+2k(x−y−z)+z−x
Donc y=−z x−y−z=x=1 et z−x=1
On trouve donc x=1,y=−2,z=2
On cherche x,y,z tels que :
bk=xak−1+ybk−1+zck−1.
On trouve x=2,y=−1, z=2
On cherche x,y,z tels que :
ck=xak−1+ybk−1+zck−1.
On trouve x=2,y=−2, z=3
On a donc :
A:=[[1,-2,2],[2,-1,2],[2,-2,3]]
Le k−ième triplet est égal à Ak*[1,0,1]
On tape :
(A^k*[1,0,1])$(k=1..6)
On obtient :
[3,4,5],[5,12,13],[7,24,25],[9,40,41],[11,60,61],[13,84,85],
[15,112,113],[17,144,145],[19,180,181],[21,220,221]
P,B:=jordan(A)
On obtient :
[[0,2,0],[4,2,0],[4,2,1]],[[1,1,0],[0,1,1],[0,0,1]]
On a Ak=PBkP−1
On sait que Bn=[[1,n,sum(k,k=1..n−1)],[0,1,n],[0,0,1]] donc on tape :
Bn:=unapply([[1,n,sum(k,k=1..n-1)],[0,1,n],[0,0,1]],n)
P*Bn(5)*inv(P)*[1,0,1]
On obtient :
[11,60,61]
On tape :
subst([2k+1,2k*(k+1),k^2+(k+1)^2],k,5)
On obtient :
[11,60,61]
On veut trouver les triangles rectangles presque isocèle de type 2.
On cherche donc les couples (a,c)∈ ℕ vérifiant 2a2+2a+1=c2.
-
Écrire un programme qui donne, en balayant tous les entiers a de 0
à n, les triplets (a,a+1,c)∈ ℕ3 vérifiant a2+(a+1)2=c2.
Donner les solutions pour n=1000
- Écrire un programme qui donne les n premiers triplés en modifiant le programme tripless (cf 1.9)
- Montrer que si le triplet (a,a+1,c)∈ ℕ3 vérifie a2+(a+1)2=c2
alors c est impair et vérifie 2c2−1=(2a+1)2.
Écrire un programme qui donne les triplets (a,a+1,c)∈ ℕ3 vérifiant a2+(a+1)2=c2 et qui utilise cette proriété de c.
- On considère la suite récurrente :
a0=0, a1=3, an+2=6an+1−an+2 (n≥ 0)
Montrer par récurrence que pour tout n∈ ℕ on a :
an+12−6anan+1+an2−2an+1−2an=3
- On considère la suite récurrente :
c0=1, c1=5, cn+2=6cn+1−cn (n≥ 0)
Montrer par récurrence que pour tout n∈ ℕ on a :
cn2=2an2+2an+1
En déduire que pour tout n∈ ℕ, les triplets (an,an+1,cn)
donnent des solutions.
On montrera dans la question 9 que l’on obtient ainsi toutes les solutions.
- Écrire un programme qui donne des triplets (a,a+1,c)∈ ℕ3
vérifiant a2+(a+1)2=c2 et qui utilise pour c la relation de
récurrence :
c0=1, c1=5, cn+2=6cn+1−cn (n≥ 0).
- On veut trouver cn en fonction de n.
Déterminer les progressions géométriques vn=v0*rn qui vérifie la
relation de vn+2=6vn+1−vn.
Puis en déduire la valeur de cn en fonction de n.
- On veut trouver an en fonction de n.
Déterminer p pour que la suite un=an+p vérifient la
relation de récurrence un+2=6un+1−un.
Puis en déduire la valeur de an en fonction de n
- Montrer que l’on a :
c0=1,a0=0 et
cn+1=4an+3cn+2
an+1=3an+2cn+1
et réciproquement si cn et an vérifient :
c0=1, a0=0, et
cn+1=4an+3cn+2
an+1=3an+2cn+1
alors
c0=1, c1=5, cn+2=6cn+1−cn (n≥ 0) et
a0=0, a1=3, an+2=6an+1−an+2 (n≥ 0)
- Montrer que l’on obtient toutes les solutions cherchèes
- Écrire la relation cn+2=6cn+1−cn sous la forme :
⎛
⎜
⎝ |
| |
| ⎞
⎟
⎠ |
=M
| ⎛
⎜
⎝ |
| |
| ⎞
⎟
⎠ |
et déterminer la matrice M
- Calculer par récurrence Mn, pour n∈ ℕ.
- On considère les suites w définies par
w0∈ ℕ, wn+1=floor((3+2√2)wn) (floor désigne la
partie entière)
Montrer qu’alors pour tout n∈ ℕ* on a :
wn+1=6wn−wn−1
En déduire que si on choisit w0=1 la suite wn est la suite
cn qui donne la longueur des hypoténuse des triangles rectangles presque
isocèles.
En déduire que si w0=1 alors 2*wn2−1 est le carré de
2an+1.
Écrire un programme qui donne les triplets (a,a+1,c)∈ ℕ3 vérifiant
a2+(a+1)2=c2 et qui utilise cette définition de c.
- Écrire les relations de récurrence :
cn=4an−1+3cn−1+2 et an=3an−1+2cn−1+1
avec une matrice 3x3.
- On considère les suites v définies par
v0∈ ℕ, vn+1=3+floor((3+2√2)vn) (floor désigne la
partie entière)
Montrer qu’alors pour tout n∈ ℕ* on a :
vn+1=6vn−vn−1+2
En déduire que si on choisit v0=0 la suite vn est la suite
an qui donne la longueur du plus petit coté des triangles rectangles
presque isocèles.
En déduire que si v0=0 et w0=1 alors 2*wn2−1=(2vn+1)2.
Écrire un programme qui donne les triplets (a,a+1,c)∈ ℕ3 vérifiant
a2+(a+1)2=c2 et qui utilise cette définition de a et c.
1.11.4 La solution de l’énoncé 2
-
On tape :
rectpiso1(n):={
local a,c,d,L;
L:=NULL;
pour a de 0 jusque n faire
d:=2a^2+2a+1;
c:=round(sqrt(d));
si c^2==d alors L:=L,[a,a+1,c];fsi;
fpour;
retourne L;
}:;
On tape :
rectpiso1(10000)
On obtient (Evaluation time: 12.73):
[0,1,1],[3,4,5],[20,21,29],[119,120,169],[696,697,985], [4059,4060,5741]
- On change le test if (gcd(m,p,q)==1) en :
if (gcd(m,p,q)==1 and abs(p-q)==1) et on tape
triplets2(n):={
local a,b,a2,b2,m,q,p,k,L;
L:=NULL;
k:=0;
a:=2;
while (k<n) {
a2:=a^2;
for (b:=1;b<a and k<n;b++) {
b2:=b^2;
m:=a2+b2;p:=a2-b2;q:=2*a*b;
if (gcd(m,p,q)==1 and abs(p-q)==1){
L:=L,[m,max(p,q),min(p,q)];
k:=k+1;
}
}
a:=a+1;
}
return L;
}:;
On tape :
triplets2(5)
On obtient :
[5,4,3],[29,21,20],[169,120,119],[985,697,696],[5741,4060,4059]
- Puisque c2=a2+(a+1)2=2a2+2a+1 on en déduit que c2 est un entier
impair donc c est un entier impair.
On a aussi :
2c2−1=4a2+4a+1=(2a+1)2
On tape :
rectpiso2(n):={
local a,c,d,L;
L:=NULL;
pour c de 1 jusque n pas 2 faire
d:=2c^2-1;
a:=round(sqrt(d));
si a^2==d alors a:=(a-1)/2; L:=L,[a,a+1,c];fsi;
fpour;
retourne L;
}:;
On tape :
rectpiso2(10000)
On obtient (Evaluation time: 5.9) :
[0,1,1],[3,4,5],[20,21,29],[119,120,169],[696,697,985], [4059,4060,5741]
- Pour n=0 on a :
an+12−6anan+1+an2−2an+1−2an=32−2*3=3
Supposons que pour n∈ ℕ on a :
an+12−6anan+1+an2−2an+1−2an=3
Calculons :
an+22−6an+1an+2+an+12−2an+2−2an+1
sachant que :
an+2=6an+1−an+2
Dans Xcas, a2 désigne an+2,a1 désigne an+1 et
a0 désigne an.
On tape :
a2:=6a1-a0+2
normal(a2^2-6a1*a2+a1^2-2a2-2a1)
On obtient :
a0^2-6*a0*a1-2*a0+a1^2-2*a1
Donc :
an+22−6an+1an+2+an+12−2an+2−2an+1=an+12−6anan+1+an2−2an+1−2an=
Donc, d’après l’hypothèse de récurrence on a :
an+22−6an+1an+2+an+12−2an+2−2an+1=3
Donc, pour tout n∈ℕ, on a :
| an+12−6anan+1+an2−2an+1−2an=3 |
- Pour n=0 on a :
c02=2a02+2a0+1=1 (puisque a0=0)
Pour n=1 on a :
c12=2a12+2a1+1=18+6+7=25 (puisque a1=3)
Supposons que pour n∈ ℕ on ait :
cn2=2an+2an+1
cn+12=2an+12+2an+1+1
Dans Xcas, c2 désigne cn+2,c1 désigne cn+1 et
c0 désigne cn.
On tape :
c2:=6c1-c0
normal(c2^2)
On obtient :
c0^2-12*c0*c1+36*c1^2
On a d’après l’hypothèse de récurrence :
c0^2=2a0^2+2a0+1 et
c1^2=2a1^2+2a0+1 :
Donc si on pose C=c2^2, on a :
C:=normal(2a0^2+2a0+1+36*(2a1^2+2a1+1)-12c0*c1)
On obtient :
2*a0^2+2*a0+72*a1^2+72*a1-12*c0*c1+37
On tape :
A:=normal(2a2^2+2a2+1)
On obtient :
-a0^2+6*a0*a1+2*a0-a1^2+2*a1+3
On veut montrer que C=A.
On tape :
normal((C-A)/12)
On obtient :
2*a0*a1+a0+a1-c0*c1+2
Il faut donc montrer que :
c0*c1=2*a0*a1+a0+a1 ou encore que :
c02*c12=(2*a0*a1+a0+a1+2)2 ou encore que :
(2a02+2a0+1)*(2a12+2a1+1)−(2*a0*a1+a0+a1+2)2=0
On tape :
normal((2a0^2+2a0+1)*(2a1^2+2a1+1)-(2*a0*a1+a0+a1+2)^2)
On obtient :
a0^2-6*a0*a1-2*a0+a1^2-2*a1-3
qui vaut bien 0 d’apres la question 2.
Donc pour tout n∈ ℕ on a cn2=2an2+2an+1=an2+(an+1)2.
Donc le triplet (an,an+1,cn) est une solution pour tout n.
On peut montrer que l’on obtient ainsi toutes les solutions (cf question9).
- On tape :
rectpiso3(n):={
local a,c,d,L,c0,c1;
c0:=1;
c1:=5;
L:=[0,1,1];
tantque c1<n faire
d:=2*c1^2-1;
a:=(sqrt(d)-1)/2;
L:=L,[a,a+1,c1];
c:=c1;
c1:=6*c1-c0;
c0:=c;
ftantque;
retourne L;
}:;
On tape :
rectpiso3(10000)
On obtient (instantanément):
[0,1,1],[3,4,5],[20,21,29],[119,120,169],[696,697,985], [4059,4060,5741]
- Si vn=v0*rn vérifie vn+2=6vn+1−vn c’est que r est solution de
x2−6x+1=0.
On tape :
r1,r2:=solve(x^2-6x+1,x)
On obtient :
[-2*sqrt(2)+3,2*sqrt(2)+3]
Donc il y a 2 progressions gépmétriques de raison r1=−2√2+3 et
r2=2√2+3 qui verifient aussi cette relation de récurence.
Une combinaison lineaire de suites verifiant
vn+2=6vn+1−vn verifient aussi cette relation de récurence.
Donc la suite :
wn=x*r1n+y*r2n vérifie wn+2=6wn+1−wn quelque soit x et y.
Puisque la suite cn est entièrement déterminée par c0=1, c1=5 et
par la relation de récurence cn+2=6cn+1−cn, pour avoir cn=wn il
suffira d’avoir c0=w0 et c1=w1 c’est à dire :
x+y=1 et x*r1+y*r2=5.
On tape :
linsolve([x+y=1,x*r1+y*r2=5],[x,y])
On obtient :
[(-(sqrt(2))+2)/4,(sqrt(2)+2)/4]
Donc :
- On cherche p pour que la suite un=p+an vérifient la
relation de un+2=6un+1−un.
On sait que an vérifie an+2=6an+1−an+2 donc p doit vérifier :
p+an+2=6p+6an+1−p−an donc p+2=6p−p.
On tape :
solve(p+2=6p-p,p)
On obtient :
[1/2]
Donc comme précédemment on va déterminer la suite an+1/2.
Pour cela on cherche x et y tel que :
x+y=a0+1/2=1/2 et x*r1+y*r2=a1=3+1/2=7/2
On tape :
normal(linsolve([x+y=1/2,x*r1+y*r2=7/2],[x,y]))
On obtient :
[(-(sqrt(2))+1)/4,(sqrt(2)+1)/4]
On a donc :
un=1−√2/4*(−2*√2+3)n+1+√2/4*(2*√2+3)n
Donc :
| an=− | | + | | *(−2* | √ | | +3)n+ | | *(2* | √ | | +3)n |
On tape :
c(n):=((-sqrt(2)+2)/4)*(-2*sqrt(2)+3)^n+
((sqrt(2)+2)/4)*(2*sqrt(2)+3)^n
a(n):=((-sqrt(2)+1)/4)*(-2*sqrt(2)+3)^n+
((sqrt(2)+1)/4)*(2*sqrt(2)+3)^n-1/2
normal(a(5),a(5)+1,c(5))
On obtient :
4059,4060,5741
On tape :
normal(a(6),a(6)+1,c(6))
On obtient :
23660,23661,33461
On tape :
normal(a(10),a(10)+1,c(10))
On obtient :
27304196,27304197,38613965
- On suppose que pour tout n ∈ ℕ on a :
c0=1, c1=5, a0=0, a1=3 et
cn+2=6cn+1−cn et
an+2=6an+1−an+2
Montrons par récurrence qu’alors pour tout n ∈ ℕ on a :
c0=1, a0=0 et
cn+1=4an+3cn+2
an+1=3an+2cn+1
La relation est vrai pour n=0 et n=1 car :
c1=4*0+3*+2=5 et
a1=3*0+2*1+1=3
Si la relation est vrai pour n on a :
cn=4an−1+3cn−1+2
an=3an−1+2cn−1+1
alors
3cn−cn−1=12an−1+8cn−1+6=4an+2
et
3an−an−1=8an−1+6cn−1+3=2cn−1
donc
cn+1=3cn+3cn−cn−1=3cn+4an+2
et
an+1=3an+3an−an−1+2=3an+2cn+1
Réciproquement si pour tout n ∈ ℕ on a :
c0=1, a0=0 et
cn+1=4an+3cn+2
an+1=3an+2cn+1
Alors :
c0=1, a0=0 et c1=4*0+3*1+2=5, a1=3*0+2*1+1=3 et
3cn+1−4an+1=cn+2
2cn+1−3an+1=−an+1
soit
4an+1=3cn+1−cn−2
2cn+1=3an+1−an+1
et puisque :
cn+2=4an+1+3cn+1+2
an+2=3an+1+2cn+1+1
on en déduit que pour tout n ∈ ℕ:
cn+2=6cn+1−cn
an+2=6an+1−an+2 - Supposons que l’on ait (a+1)2+a2=2a2+2a+1=c2.
Alors c est impair et a et c sont premiers entre eux.
On a aussi : 2c2=(2a+1)2+1
Si a est pair
0n a :
(a+1)2=c2−a2=(c+a)(c−a)
donc si d divise a+1, d divise soit c+a, soit c−a mais d ne divise
pas c+a et c−a car a et c sont premiers entre eux donc :
il existe p et q tel que c+a=p2 et c−a=p2 et pq=a+1
On a donc p≥ q avec p et q sont impairs et,
2a=p2−q2 et 2c=p2+q2.
La relation 4c2=8a2+8a+4 donne comme relation entre p et q :
(p2+q2)2=2(p2−q2)2+4(p2−q2)+4
donc
p4+q4−6p2q2+4p2−4q2+4=0
Posons
X=p2
Y=q2
X et Y sont des carrés d’entiers qui vérifient :
Y2−2Y(2+3X)+(X+2)2
Le discriminant de ce trinôme en Y est donc le carré d’un entier, c’est
à dire 2X+2 est le carré d’un entier puisque :
(2+3X)2−(X+2)2=8X2+8X=(2p)2(2X+2).
En posant p=2*p1+1 on en déduit que X=4p12+4p1+1 et que
2X+2=8p12+8p1+4=4(2p12+2p1+1) et donc qu’il existe
k ∈ ℕ tel que :
2p12+2p1+1=k2
et on a alors :
Y=q2=(2+3p2)−4kp (avec le signe "-" car q< p)
donc si 2a2+2a+1=c2 avec a est pair, il existe p avec p=2*p1+1 et
k vérifiant 2p12+2p1+1=k2 (ou 2k2=p2+1) tel que :
2a=p2−q2=X−Y=4kp−2−2p2=4kp−4k2=4k(p−k)
2c=p2+q2=X+Y=4p2+2−4kp=8k2−4kp−2=2(4k2−2kp−1)
Réciproquent si on a 2p12+2p1+1=k2 pour p1 ∈ ℕ* et k ∈ ℕ
alors si on pose p=2*p1+1 on a 2k2=(2p1+1)2+1=p2+1 et :
a=2kp−1−p2=2k(p−k)
c=4k2−2kp−1
a est pair a>p1>0, c>k et on vérifie que 2a2+2a+1=c2, pour cela,
on tape :
a:=2k*p-k^2
c:=4k^2-1-2k*p
factor(2a^2+2a+1-c^2)
On obtient :
2*p^2*(2*k^2-p^2-1)
Donc puisque 2k2=p2+1 on a 2a2+2a+1=c2
Si a est impair alors a+1 est pair
0n fait le même genre de raisonnement :
a2=c2−(a+1)2=(c+a+1)(c−a−1)
donc si d divise a, d divise soit c+a+1, soit c−a−1 mais d ne
divise pas c+a+1 et c−a−1 car a et c sont premiers entre eux donc :
il existe p et q tel que c+a+1=p2 et c−a−1=p2 et pq=a.
On a p≥ q et p et q sont impairs et,
2a=p2−q2−2 et 2c=p2+q2.
Posons
X=p2
Y=q2
X et Y sont des carrés d’entiers qui vérifient :
X2−2X(2+3Y)+(Y+2)2
(même équation en échangeant Y et X)
2Y+2 est un carré en posant q=2q1+1 cela veut dire qu’il existe
r ∈ ℕ tel que : 2q12+2q1+1=r2 ou encore 2r2=q2+1
et alors X=3Y+2+4qr=3q2+2+4qr (avec le signe "+" car X=p2>q2)
donc:
2a=p2−q2−2=2q2+4qr=2(q2+1)−2+4qr=2(2r2+2qr−1)
2c=p2+q2=4q2+4qr+2=4(q2+1)−2+4qr=2(4r2+2qr−1)
Réciproquent si on a 2q12+2q1+1=r2 pour q1 ∈ ℕ et r ∈ ℕ
alors si on pose q=2*q1+1 on a 2r2=(2q1+1)2+1=q2+1 et :
a=2r2+2qr−1
c=4r2+2qr−1
a est impair et on tape :
a:=2r^2+2q*r-1
c:=4r^2+2q*r-1
factor(2a^2+2a+1-c^2)
On obtient :
2*q^2*(2*r^2-q^2-1)
Donc puisque 2r2=q2+1 on a 2a2+2a+1=c2.
Conclusion
Si a1,c1 est une solution de 2a2+2a+1=c2 alors cette solution engendre
2 nouvelles solutions qui sont :
a2=2c1(2a1−c1+1) et c2=(2a1+1)2+2c1(c1−2a1−1)
a3=(2a1+1)2+2(2a1+1)c1 et c3=2(2a1+1)2+2(2a1+1)c1+1
puis la solution a2,c2 engendre 2 nouvelles solutions qui sont :
a4=2c2(2a2+1−c2) et c4=(2a2+1)2+2c2(c2−2a2−1)
a5=(2a2+1)2+2(2a2+1)c2 et c5=2(2a2+1)2+2(2a2+1)c2+1
On remarquera que la solution [0,1] engendre [0,1] et [3,5], que la
solution s1=[3,5] engendre s2=[20,29] et s3=[119,169] etc...par ce
processus la solution sn engendre les solutions s2n et s2n+1, puis
la solution sn+1 engendre les solutions s2n+2 et s2n+3 etc...
Pour faire le lien avec les suites précédentes, il reste a montrer que la
suite [an,cn] ainsi engendrée vérifie :
cn=4an−1+3cn−1+2 et an=3an−1+2cn−1+1
On utilise Xcas pour faire les calculs.
Si sn=[a,c] et sn+1=a1,c1) sont des solutions successives,
on désigne s2n par [sa1(a,c),sc1(a,c)], s2n+1 par [sa2(a,c),sc2(a,c)] et s2n+2 par [sa1(a1,c1),sc1(a1,c1)].
On désigne par rc(a,c) et par ra(a,c) les relations de
récurrence qui donne cn+1 et an+1 en fonction de an et cn.
On suppose que les relations de récurrence sont vérifiées par sn et
sn+1 i.e. que a1=ra(a,c) et c1=rc(a,c).
On tape les définitions :
sa1(a,c):=normal(4*c*a+2*c-2*c^2)
sc1(a,c):=normal(4*c^2-4*c*a-2*c-1)
sa2(a,c):=normal(4*c*a+2*c-1+2*c^2)
sc2(a,c):=normal(4*c^2+4*c*a+2*c-1)
rc(a,c):=4*a+3*c+2;
ra(a,c):=3*a+2*c+1
On tape :
normal(rc(sa1(a,c),sc1(a,c))-sc2(a,c))
On obtient : 0
On tape :
normal(ra(sa1(a,c),sc1(a,c))-sa2(a,c))
On obtient : 0
On tape :
factor(ra(sa2(a,c),sc2(a,c))-sa1(ra(a,c),rc(a,c)))
On obtient : -8*(2*a^2+2*a-c^2+1)
On tape :
factor(rc(sa2(a,c),sc2(a,c))-sc1(ra(a,c),rc(a,c)))
On obtient : -8*(2*a^2+2*a-c^2+1)
ce qui donne bien 0 puisque 2a2+2a+1=c2 car sn=[a,c] est
une solution de cette équation par hypothèse.
On a ainsi montrer que si :
sn=[a,c] et sn+1=a1,c1) sont des solutions successives qui
vérifient les relations de récurrence alors s2n, s2n+1, s2n+2 vérifient aussi les relations de récurrence.
s1=[3,5] engendre s2=[20,29] et s3.
On peut vérifier par le programme de la question 1 que [3,5] et [20,29]
sont 2 solutions successives qui vérifie la relation de récurrence
(29=4*3+3*5+2 et 20=3*3+2*5+1) donc on en déduit par récurrence que :
si s2 engendre s4et s5, alors s2,s3,s4 sont des solutions
successives qui vérifient la relation de récurrence....
On peut aussi faire le programme suivant qui renvoie la liste des solutions en
utilisant les fonctions sa1, sc1, sa2, sc2 définies précédemment :
sa1(a,c):=normal(4*c*a+2*c-2*c^2);
sc1(a,c):=normal(4*c^2-4*c*a-2*c-1);
sa2(a,c):=normal(4*c*a+2*c-1+2*c^2);
sc2(a,c):=normal(4*c^2+4*c*a+2*c-1);
tripisoc(n):={
local a,a1,a2,c,c1,c2,L,k;
L:=[0,1],[3,5];
pour k de 1 jusque n faire
a,c:=L[k];
L:=L,[sa1(a,c),sc1(a,c)],[sa2(a,c),sc2(a,c)];
fpour;
return L;
}:;
- 0n a :
cn+2=6cn+1−cn et
cn+1=cn+1
donc
- Si
On a :
p0=1, q0=0, s0=0, t0=1,
p1=6, q1=−1, s1=1, t0=0
Mn+1=M*Mn c’est à dire :
pn+1=6pn−sn, qn+1=6qn−tn, sn+1=pn, tn+1=qn
donc
pn+1=6pn−pn−1 avec p0=1 et p1=6
qn+1=6qn−qn−1 avec q0=0 et q1=−1
Les suites pn et qn vérifient la même relation de récurrence que
cn donc :
pn et qn sont des combinaisons linéaires des 2 progressions géométriques de raison r1=−2√2+3 et r2=2√2+3.
Calcul de pn=x(r1)n+y(r2)n
Pour trouver pn en fonction de n il faut donc résoudre :
[x+y=1=p0,x*r1+y*r2=6=p1]
On tape :
r1,r2:=solve(x^2-6x+1,x)
On obtient :
[-2*sqrt(2)+3,2*sqrt(2)+3]
On tape :
linsolve([x+y=1,x*r1+y*r2=6],[x,y])
On obtient :
[(-3*sqrt(2)+4)/8,(3*sqrt(2)+4)/8]
Calcul de qn=x(r1)n+y(r2)n
Pour trouver qn en fonction de n il faut donc résoudre :
[x+y=0=q0,x*r1+y*r2=1=q1]
On tape :
linsolve([x+y=0,x*r1+y*r2=1],[x,y])
On obtient :
[(-(sqrt(2)))/8,(sqrt(2))/8]
Donc pour n∈ ℕ :
pn=(−3√2+4)(−2√2+3)n+(3√2+4)(2√2+3)n
qn=−√2(−2√2+3)n+√2(2√2+3)n - On peut aussi écrire la relation de récurrence :
cn=4an−1+3cn−1+2
an=3an−1+2cn−1+1
en utilisant A une matrice 3x3 :
et ainsi, on a :
⎛
⎜
⎜
⎝ |
| |
| ⎞
⎟
⎟
⎠ |
=A
| ⎛
⎜
⎜
⎝ |
| |
| ⎞
⎟
⎟
⎠ |
On a donc :
⎛
⎜
⎜
⎝ |
| |
| ⎞
⎟
⎟
⎠ |
=An
| ⎛
⎜
⎜
⎝ |
| |
| ⎞
⎟
⎟
⎠ |
On vérifie en tapant :
normal(rsolve([a(n+1)=3*a(n)+2*c(n)+d(n),
c(n+1)=4*a(n)+3*c(n)+2*d(n),
d(n+1)=d(n)],[a(n),c(n),d(n)],[a(0)=0,c(0)=1,d(0)=1]))
On obtient :
[[(-(sqrt(2))+1)/4*(-2*sqrt(2)+3)^n+
(sqrt(2)+1)/4*(2*sqrt(2)+3)^n+(-1)/2,
(-(sqrt(2))+2)/4*(-2*sqrt(2)+3)^n+
(sqrt(2)+2)/4*(2*sqrt(2)+3)^n,
1]]
- On considère la suite :
w0∈ ℕ*, wn+1=floor(3+2*√2)*wn) (floor désigne la partie
entière)
On veut montrer que pour tout n∈ ℕ* on a wn+1+wn−1=6wn.
On a :
wn+1≤ (3+2*√2)*wn<wn+1+1
Donc :
(3+2*√2)*wn−1<wn+1≤ (3+2*√2)*wn
On a :
wn≤ (3+2*√2)*wn−1<wn+1
Puisque 1/3+2*√2=3−2*√2 on a :
wn*(3−2*√2)≤ wn−1)<(wn+1)*(3−2*√2)
Donc :
(3+2*√2)*wn−1+wn*(3−2*√2)<wn+1+wn−1<(3+2*√2)*wn+(wn+1)*(3−2*√2)
Donc :
6wn−1<wn+1+wn−1<6wn+(3−2*√2)<6wn+1.
Comme wn+1+wn−1 est un entier, on en déduit qwe :
wn+1+wn−1=6wn.
Pour montrer que wn est la suite cn il suffit de montrer que w1=5
lorsque w0=1.
On a bien w1=floor(3+2*√2)=5, donc wn et cn coincident.
On tape :
rectpiso5(n):={
local a,c,d,L;
L:=NULL;
c:=1;
tantque c<n faire
d:=2*c^2-1;
a:=(sqrt(d)-1)/2;
L:=L,[a,a+1,c];
c:=floor((3+2*sqrt(2))*c);
ftantque;
retourne L;
}:;
On tape :
rectpiso4(10000)
On obtient (instantanément) :
[0,1,1],[3,4,5],[20,21,29],[119,120,169],[696,697,985], [4059,4060,5741]
- On considère la suite :
v0∈ ℕ*, vn+1=floor(3+2*√2)*wn)+3 (floor désigne la partie
entière)
On veut montrer que pour tout n∈ ℕ* on a vn+1+vn−1=6wn+2.
On a :
vn+1≤ (3+2*√2)*vn+3<vn+1+1
Donc :
(3+2*√2)*vn+2<vn+1≤ (3+2*√2)*vn+3
On a :
vn≤ (3+2*√2)*vn−1+3<vn+1
Puisque 1/3+2*√2=3−2*√2 on a :
(vn−3)*(3−2*√2)≤ vn−1)<(vn−2)*(3−2*√2)
Donc :
(3+2*√2)*vn+2+(vn−3)*(3−2*√2)<vn+1+vn−1<(3+2*√2)*vn+3+(vn−2)*(3−2*√2)
Donc :
6vn+1<6vn+2−9+6*√2<vn+1+vn−1<6wn+(3−6+4*√2)<6vn+3.
Comme vn+1+vn−1 est un entier, on en déduit qwe :
vn+1+vn−1=6vn+2.
Pour montrer que vn est la suite an il suffit de montrer que v1=3
lorsque v0=0.
On a bien v1=floor((3+2*√2)*0)+3=3, donc vn et an coincident.
On tape :
rectpiso5(n):={
local a,c,d,L;
L:=NULL;
c:=1;
a:=0;
tantque c<n faire
L:=L,[a,a+1,c];
c:=floor((3+2*sqrt(2))*c);
a:=floor((3+2*sqrt(2))*a)+3;
ftantque;
retourne L;
}:;
On tape :
rectpiso5(10000)
On obtient (instantanément) :
[0,1,1],[3,4,5],[20,21,29],[119,120,169],[696,697,985], [4059,4060,5741]



 On tape :
On tape :



