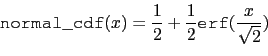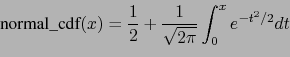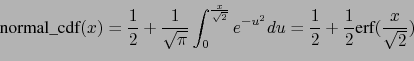Error function : erf

suivant: Complementary error function: erfc monter: Real numbers précédent: n-th root : root Table des matières Index

Error function : `erf`

erf takes as argument a number a.
erf returns the floating point value of the error function at x = a, where the error function is defined by :

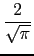
erf(x) = 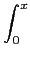$\displaystyle {\frac{{2}}{{\sqrt{\pi}}}}$ $\displaystyle \int_{0}^{{x}}$ e^-t²dt

The normalization is choosen so that:

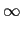
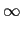
erf(+ $\displaystyle \infty$ ) = 1, erf(- $\displaystyle \infty$ ) = - 1

since :

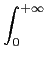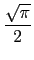
$\displaystyle \int_{0}^{{+\infty}}$ e^-t²dt = $\displaystyle {\frac{{\sqrt{\pi}}}{{2}}}$

Input :

erf(1)

Output :

0.84270079295

Input :

erf(1/(sqrt(2)))*1/2+0.5

Output :

0.841344746069

Remark
The relation between erf and normal_cdf is :

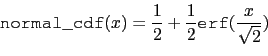
$\begin{displaymath}\mbox{\tt normal\_cdf}(x)=\frac{1}{2}+\frac{1}{2}\*\mbox{\tt erf}(\frac{x}{\sqrt{2}}) \end{displaymath}$

Indeed, making the change of variable t = u*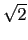 $\sqrt{{2}}$ in

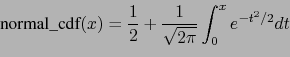
$\begin{displaymath}\mbox{normal\_cdf}(x)=\frac{1}{2}+\frac{1}{\sqrt{2\pi}}\int_0^{x}e^{-t^2/2}dt\end{displaymath}$

gives :

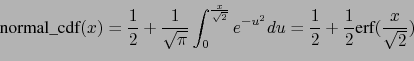
$\begin{displaymath}\mbox{normal\_cdf}(x)=\frac{1}{2}+\frac{1}{\sqrt{\pi}}\int_0^... ...-u^2}du=\frac{1}{2}+\frac{1}{2}\*\mbox{erf}(\frac{x}{\sqrt{2}})\end{displaymath}$

Check :
normal_cdf(1)=0.841344746069

giac documentation written by Renée De Graeve and Bernard Parisse