




suivant: Differential equations
monter: Linear systems
précédent: Linear system solving: linsolve
Table des matières
Index
Finding linear recurrences : reverse_rsolve
reverse_rsolve takes as argument a vector
v = [v0...v2n-1] made of the first 2n terms of a sequence (vn)
which is supposed to verify a linear recurrence relation of
degree smaller than n
xn*vn+k + ... + x0*vk = 0
where the xj are n + 1 unknowns.
reverse_rsolve returns the list
x = [xn,..., x0]
of the xj coefficients (if xn 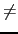 0 it is reduced to 1).
0 it is reduced to 1).
In other words reverse_rsolve solves the linear system of
n equations :
| xn*vn + ... + x0*v0 |
= |
0 |
|
| ... |
|
|
|
| xn*vn+k + ... + x0*vk |
= |
0 |
|
| ... |
|
|
|
| xn*v2*n-1 + ... + x0*vn-1 |
= |
0 |
|
The matrix A of the system has n rows and n + 1 columns :
A = [[v0, v1...vn],[v1, v2,...vn-1],...,[vn-1, vn...v2n-1]]
reverse_rsolve returns the list
x = [xn,...x1, x0] with xn = 1
and x is the solution of the system
A* (x).
(x).
Examples
- Find a sequence verifying a linear recurrence of degree at
most 2 whose first elements 1, -1, 3, 3.
Input :
reverse_rsolve([1,-1,3,3])
Output :
[1,-3,-6]
Hence x0 = - 6, x1 = - 3, x2 = 1 and the recurrence relation is
vk+2 -3vk+1 -6vk = 0
Without reverse_rsolve, we would write the matrix of the system :
[[1,-1,3],[-1,3,3]] and use the rref command :
rref([[1,-1,3],[-1,3,3]])
Output is [[1,0,6],[0,1,3]] hence x0 = - 6 and x1 = - 3
(because x2 = 1).
- Find a sequence verifying a linear recurrence of degree at
most 3 whose first elements are 1, -1, 3, 3,-1, 1.
Input :
reverse_rsolve([1,-1,3,3,-1,1])
Output :
[1,(-1)/2,1/2,-1]
Hence so, x0 = - 1, x1 = 1/2, x2 = - 1/2, x3 = 1, the recurrence
relation is
vk+3 -
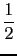 vk+2
vk+2 +
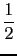 vk+1
vk+1 -
vk = 0
Without reverse_rsolve, we would write the matrix of the system :
[[1,-1,3,3],[-1,3,3,-1],[3,3,-1,1]].
Using rref command, we would input :
rref([[1,-1,3,3],[-1,3,3,-1],[3,3,-1,1]])
Output is [1,0,0,1],[0,1,0,1/-2],[0,0,1,1/2]]
hence x0 = - 1, x1 = 1/2 and x2 = - 1/2 because x3 = 1),





suivant: Differential equations
monter: Linear systems
précédent: Linear system solving: linsolve
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
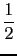 vk+2 +
vk+2 + 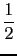 vk+1 - vk = 0
vk+1 - vk = 0