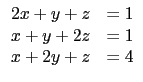



suivant: Finding linear recurrences :
monter: Linear systems
précédent: Step by step Gauss-Jordan
Table des matières
Index
Linear system solving: linsolve
linsolve is used to solve a system of linear equations.
linsolve has two arguments: a list of equations or
expressions (in that case the convention is that the equation
is
expression = 0), and a list of variable names.
linsolve returns the solution of the system in a list.
Input :
linsolve([2*x+y+z=1,x+y+2*z=1,x+2*y+z=4],[x,y,z])
Output :
[1/-2,5/2,1/-2]
Which means that
is the solution of the system :
giac documentation written by Renée De Graeve and Bernard Parisse