




suivant: Jacobi symbol : jacobi_symbol
monter: Integers (and Gaussian Integers)
précédent: The Euler indicatrix :
Table des matières
Index
Legendre symbol : legendre_symbol
If n is prime, we define the Legendre symbol of a
written
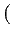
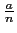
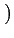 by :
by :
Some properties
legendre_symbol takes two arguments a and n and returns the Legendre
symbol
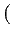
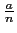
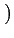 .
.
Input :
legendre_symbol(26,17)
Output :
1
Input :
legendre_symbol(27,17)
Output :
-1
Input :
legendre_symbol(34,17)
Output :
0
giac documentation written by Renée De Graeve and Bernard Parisse

