Gröbner reduction : greduce

greduce has three arguments : a multivariate polynomial, a vector made of polynomials which is supposed to be a Gröbner basis, and a vector of variable names.
greduce returns the reduction of the polynomial given as first argument with respect to the Gröbner basis given as the second argument. It is 0 if and only if the polynomial belongs to the ideal.

Input :

greduce(x*y-1,[x^2-y^2,2*x*y-y^2,y^3],[x,y])

Output :

y^2-2

that is to say xy - 1 = 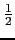${\frac{{1}}{{2}}}$(y² -2)  mod I where I is the ideal generated by the Gröbner basis [x² - y², 2xy - y², y³], because y² - 2 is the euclidian division rmainder of 2(xy - 1) by G₂ = 2xy - y².

Like gbasis (cf. 1.27.1), greduce may have more than 3 arguments to specify ordering and algorithm if they differ from the default (lexicographic ordering). Input :

greduce(x1^2*x3^2,[x3^3-1,-x2^2-x2*x3-x3^2,x1+x2+x3], [x1,x2,x3],tdeg)

Output

x2