Gröbner basis : gbasis

gbasis takes at least two arguments

• a vector of multivariate polynomials
• a vector of variables names,

Optionnal arguments may be used to specify the ordering and algorithms. By default, the ordering is lexicographic (with respect to the list of variable names ordering) and the polynomials are written in decreasing power orders with respect to this order. For example, the output will be like ... + x²y⁴z³ + x²y³z⁴ + ... if the second argument is [x, y, z] because (2, 4, 3) > (2, 3, 4) but the output would be like ... + x²y³z⁴ + x²y⁴z³ + ... if the second argument is [x, z, y].
gbasis returns a Gröbner basis of the polynomial ideal spanned by these polynomials.

Property
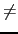If I is an ideal and if (G_k)_{k $\in$ K} is a Gröbner basis of this ideal I then, if F is a non zero polynomial in I, the greatest monomial of F is divisible by the greatest monomial of one of the G_k. In other words, if you do an euclidian division of F $\neq$ 0 by the corresponding G_k, take the remainder of this division, do again the same and so on, at some point you get a null remainder.

Input :

gbasis([2*x*y-y^2,x^2-2*x*y],[x,y])

Output :

[4*x^2+-4*y^2,2*x*y-y^2,-(3*y^3)]

As indicated above, gbasis may have more than 2 arguments :

• plex (lexicographic only), tdeg (total degree then lexicographic order), revlex (total degree then inverse lexicographic order), to specify an order on the monomials (plex is the order by default),
• with_cocoa=true or with_cocoa=false, if you want to use the CoCoA library to compute the Gröbner basis (recommended, requires that CoCoA support compiled in)

• with_f5=true or with_f5=false for using the F5 algorithm of the CoCoA librairy . In this case the specify order is not used (the polynomials are homogeneized).

Input :

gbasis([x1+x2+x3,x1*x2+x1*x3+x2*x3,x1*x2*x3-1], [x1,x2,x3],tdeg,with_cocoa=false)

Output

[x3^3-1,-x2^2-x2*x3-x3^2,x1+x2+x3]