«Harmonics» project

Alex, Bo, Fred, Malik

2024, july 8th

image: 2_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_IDEX_france2030_couleur.jpg

Abstract

Tonnetz is software developed by Frédéric Faure, Malik Mezzadri, Alexandre Ratchov and Bo VanderWerf. Tonnetz is aimed to play music with just intonation, with MIDI instruments and also with acoustic instruments, via microphone. It also controls a slider-flute. It contains an automate that can play, according to a Markov graph.

This document is a tutorial. It explains different aspects of the program tonnetz, from installation in 1, to the abstract concepts and practical use. There is an other document called “reference” that gives all mathematical details and software code explanations. The objective of this program “Tonnetz” are multiple: from research in musicology, pedagogical use, to compose music, play and improvise on stage.

1 Installation of plugin Tonnetz and softwares on the computer Mac-Os

2 How to use

2.1 Program Tonnetz (StandAlone)

3 Versions and news

4 Sessions passées

5 Objectives of the project

5.1 First ojectives

5.2 Some conferences?

5.3 Objectives

6 Pedagogical tutorial: how to start with the plugin tonnetz

6.1 Summary of the tonnetz plugin with few key-words

7 Theoretical description

7.1 Harmonics and just intervals

7.2 Tunplot: the pitch space

7.3 Netplot: the tonnetz space

7.4 Formula for pitch values

7.5 Temperaments

8 Some examples of just intervals, just chords and chord progressions

8.1 Great cadence

9 Advanced use of the plugin

9.1 Automation

9.2 Adaptative temperament with different N_keys and levels

9.3 Many musicians, how to use in session

A EWI

A.1 EWI USB

A.2 EWI 5000

Remark 0.1. you can click on the colored words, they contain an hyper-link to wikipedia or other multimedia contents.

This tutorial assumes some basic knowledge in music, but no knowledge in mathematics. If some parts are not understandable, the reader can skip them (and also mail to the author, thanks). The reader can begin by looking at the different videos given as examples in the links.

Documents and references:

Official presentation of the project (or here in french).

1 Installation of plugin Tonnetz and softwares on the computer Mac-Os

If not already done, download Synth that contains the sounds for the synthetizer 'midisyn' of Alex.
Download the latest version of the plugin Tonnetz.
- If MacOs refuse to install, go to directory Downloads, use the key Ctrl and left clic on the file and Open it in the menu

2 How to use

2.1 Program Tonnetz (StandAlone)

Start:
- In Applications/Fred/Tonnetz
Settings:
- in the upper left corner: Options/Audio_midi_settings/Audio_buffer_size: choose 128 samples and in Active_MIDI_Inputs: connect your device (EWI or Keyboard).

3 Versions and news

21/01/2024, version 1.1.1

Version simplifiée du plugin Tonnetz qui permet de:

Jouer avec l'ewi ou clavier. Choisir le son dans 'audio out'. Choisir le tempérament.
Avec l'ewi, passer/sortir du mode 'hold' en mordant un peu et effacer les notes en mordant fort. Il y a une jauge 'crunch' qui montre le seuil. Ainsi, en mode hold, on peut poser des accords.
Si on rejoue une note existante, cela l'éteind.
On peut jouer sur differents canaux de l'EWI, par exemple
- canal 1: en mode hold pour construire des accords,
- canal 2: en mode hold off, pour jouer un solo.
On peut modifier les accords avec la souris, en cliquant sur les notes (on/off) et modifier la force des notes avec la molette.
Save/Load des accords et faire evoluer des accords en choisissant différents paramètres.
Jouer en temperament adaptatif ou fixe et décaler les tempéraments fixes selon les directions $3, 5, 7$ .

19/02/2024, version 1.1.9

Il y a un seul package appelé Tonnetz qui contient:
- Tonnetz_Synth qui est un synthétizer for LogicPro or GarageBand, etc. This is an AU Plugin.
  The suffix Synth means “synthetizer” and that on output it gives some sounds from an internal synthetizer (by Alex or Fred).
- Tonnetz_MidiFX est un plugin for LogicPro, this is a AU Plugin.
  The suffix MidiFX means “midi effect” and that on output it gives midi events. Beware that it is not accepted by GarageBand. On LogicPro, to have sound, you need to put after this plugin, any external synthetizer which accepts pitch-bend and calibrate the pitch bend to the range $\pm 2$ (e.g. Diva).
- Tonnetz_Analyzer is for LogicPro or GarageBand, etc. This is an AU Plugin.
  The suffix Analyzer means “audio effect” and that on input and output it takes some audio. on peut jouer avec un instrument acoustique et en particulier la flute à coulisse.

19/02/2024, version 1.1.10

Dans la section, “1 Temperaments/ 3 Display Settings”, un mot de passe est requis pour accéder à l'onglet “8 For developpers”.
Représentation en portée musicale “Staff” dans “1 Temperaments/ 3 Display Settings”.
On peut éditer un tempérament fixe dans la section “1 Temperaments/5 Edit”
- Il faut au préalable sélectionner un tempérament fixe.
- On modifie les notes, soit à la souris sur la fenetre tunplot ou la fenetre netplot, soit avec les widgets.
- Penser à utiliser le bouton droit de la souris pour basculer en mode freeze.
On peut sauvegarder et rejouer des accords dans la section “1 Temperaments/2 Chords/ 1 Save/Load” et faire évoluer les accords dans la section “1 Temperaments/2 Chords/ 2 Change Chord”
Si on utilise un synthe extérieur avec le plugin Tonnetz_MidiFx, on peut tester si le synthe (par Diva) est bien configuré pour les messages de microtonalité, avec le bouton de la section “2 Midi / Midi out / External Synth/ Test Pitch bend”.

20/04/2024, version 1.1.12

Une version StandAlone du programme que l'on peut utiliser directement dans Applications/Fred/Tonnetz

23/05/2024, version 1.1.13

On peut programmer et faire jouer un automate dans la section “4 Markov Automate”. Il composera en direct selon des suites d'instructions situées sur les sommets d'un graphe de Markov.

21/07/2024, version 1.1.16

Il y a une interface graphique (comme des pads) pour jouer la suite d'accords: dans “1_Tempéraments/2_Chords/Show_sequence”.

4 Sessions passées

quelques enregistrements.

5 Objectives of the project

5.1 First ojectives

5.1.1 For Alex & Fred

Developp the plugin «tonnetz», midi->midi:
- that works as a AU plugin on MacOs, in LogicPro or Ardour or Reaper and explain how to use it.
- We could use the plugin tonnetz with an EWI (or MIDI keyboard) to record some multiple Midi tracks with chords and get sound from any synthetizer.
- Connect «tonnetz» with Alex's plugin synthetizer «midisyn» (midi->audio) to get the special sounds and effects of Alex.
- Connect «tonnetz» with a plugin «pitch-detection» (audio->midi) so that Malik can use its «flute à coulisse» or flute or voice or «flute à nez»,
Developp the plugin «midisyn» (synthetizer midi->audio).
Developp the plugin «pitch-detection» (audio->midi).
Developp the plugin «markov» (midi->midi) that interacts with «tonnetz» and allow to generates some midi patterns followings rules from Markov graphs.
In order to simplify the use for musicians, propose a unified plugin (audio,midi-> audio, midi) that contains all the previous plugins.

5.1.2 For Bo & Malik

Use the plugins to compose and record music.

5.1.3 Together (Alex, Bo, Fred, Malik)

Also with Paul Albenge and Aline, we meet together, in order to prepare a concert and some support: audio record documentary, ...

5.2 Some conferences?

Une conférence sur les tempéraments anciens et actuels?

5.3 Objectives

Un disque
Documentaire de 15' + 30' de morceaux

6 Pedagogical tutorial: «how to start with the plugin tonnetz»

Before starting to use the plugin tonnetz let us give a short introduction that gives an idea of “what tonnetz is” and a few important “key words” for after.

6.1 Summary of the tonnetz plugin with few key-words

6.1.1 MIDI,Audio, DAW and plugins

Audio signal means a sound that has been transformed to a sequence of numbers (i.e. digitized).
- the time is cut in small intervals $δ = \frac{1}{F}$ , e.g. $F = 44100$ Hz intervals in a second called the rate frequency.
- The amplitude is also approximated by integers in the interval $(- 2^{B - 1}, 2^{B - 1} - 1)$ with integer $B$ called the bit sampling, ex: $B = 4$ in the picture below but usually we take $B = 32$ for good precision.
MIDI signal is a sequence of numbers that represent some instructions between musical devices (keyboards, computer, etc) in electronic music.
- The list of all instructions is defined by the MIDI association.
- For example the note $C$ with maximal volume is represented by the sequence of numbers ${144, 60, 127}$ (here $144$ means 'note on', $60$ means 'C' and $127$ is the maximal value).
A DAW means Digital Audio Workstation and is a software in a computer that acts as a “recorder”. It allows to record some audio signals and MIDI signals on tracks and play these tracks on output speakers.
- We will mainly use Ardour, that is a efficient and free software. However most of professionals use Protools on windows PC or Logic-Pro on MacOs (these are proprietary software).
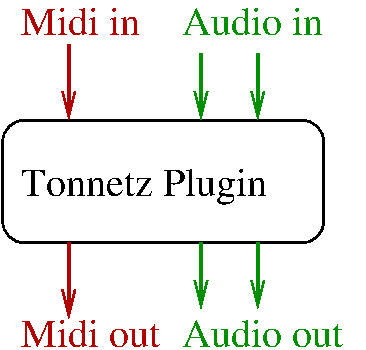
An audio plugin is a computer software that can be used in a DAW for transforming Audio signals (and/or) MIDI signals. In our case, “tonnetz” is a plugin that takes audio (stereo) and MIDI on input and output:

6.1.2 The tonnetz

By definition, the tonnetz is the space of all notes with rational frequency ratios, i.e. fraction, called just intervals in music, starting from an arbitrary original note which is the "diapason" (A at 440 Hz). In principle, this space of "just notes" is accessible to all musicians simultaneously. But this note space is infinite - there are even infinitely many notes between each note, just like the rational numbers Q. See this short video on numbers. Because of this infinity, in practice, we have to use a temperament to access some of these "just notes".
For a musician, a temperament is a limited number of tonnetz notes to which he has access, via the keys of his instrument (C,C#,C etc). In other words, a temperament is a choice of just notes. There are two types of temperament:
- fixed temperament, where the choice is fixed during the play. You can use a predefined fixed temperament, such as the (historical) fixed temperaments of Zarlino, Pythagoras, Harmonic, etc. (and their transpositions), or use a personal customized fixed temperament.
- an adaptive temperament, where this choice depends on the leader notes present (played by all leader musicians). This guaranties a better coherence in the harmony.
A musician is in leader mode if the notes he plays and holds influence the adaptive temperaments of the other musicians and himself. Otherwise, the musician is said to be in follower mode.

Remark 6.1. if several musicians are playing together, it's possible for each musician to use his or her own temperament. For example, “musician red” uses an adaptive temperament and “musician blue” uses a fixed temperament (in mode leader or follower). Later each musician or plugin will be identified by a color.

7 Theoretical description

7.1 Harmonics and just intervals

7.1.1 Human voice and importance of harmonics and just intervals

Human voice is created by the periodic vibration of vocal cords. From Fourier analysis, there are harmonics in every periodic signal like the human voice, a sound of a string instrument, a flute or a trumpet, etc. Harmonics are therefore present in the human voice and other musical sounds.

Just intervals are the intervals between different harmonics. Our brain is well trained to analyze and recognize human voice via identification of these just intervals, so we can understand that just intervals play an important role in music. This is what we will be concerned with this program.

Auditive illusion:

This video (read the given description) illustrates how the brain creates virtual fundamentals from just intervals, as it would like to give the information to consciousness that a human voice is present. See wikipedia about Missing fundamental.

7.1.2 What are the harmonics

The harmonics of the fundamental note

C_{3}

for example (subscript

3

here means octave

3

), is the following series of notes (and correction in half-tone)

image: 5_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_harmonics.png

where the index is the harmonic number

1, 2, 3, \dots

and the subscript is the correction with respect to the equal temperament. For example, harmonic 3 is

G

with a correction

+ 0.02

of halftone. Harmonic

7

B ♭

with a correction

- 0.31

of halftone, that is very perceptible. What is important to observe and enough to remember for after is:

Harmonic $1$ is called the fundamental.
Harmonic $2$ is an octave from the fundamental.
Harmonic $3$ is a fifth (plus an octave) from the fundamental with $+ 0.02$ of halftone (not perceptible).
Harmonic $5$ is a major third (plus two octaves) from the fundamental with $- 0.14$ of halftone.
Harmonic $7$ is a minor seventh (plus two octaves) from the fundamental with $- 0.31$ of halftone.
Harmonic $11$ is a augmented fourth (plus three octaves) from the fundamental with $- 0.49$ of halftone.
Harmonic $13$ is a major sixth (plus three octaves) from the fundamental with $+ 0.40$ of halftone.

Numbers

2, 3, 5, 7, \dots

are prime numbers and are enough to construct every other numbers, e.g. harmonic

6 = 2 \times 3

is one octave above harmonic

3

, hence

2

octaves and a fifth above the fundamental. Harmonic

9 = 3 \times 3

is a fifth and an octave above harmonic

3

, hence two octaves and two fifth above the fundamental, etc.

Frequency of the harmonics:

f = f_{C_{3}}

is the frequency of the fundamental, then the frequency of harmonic

3

f_{G_{4}} = 3 f

, and frequency of harmonic

5

f_{E_{5}} = 5 f

, etc. These frequencies are slightly different from the frequency obtained in equal temperament (more on this below). More informations about harmonics are in the appendix sec:Harmonics.

7.1.3 What are just intervals

Between the first harmonics, there are the following intervals:

a fourth between harmonics $3 \to 4$ ,
a minor third ( $+ 0.16$ ) between harmonics $5 \to 6$ ,
another different minor third ( $- 0.29$ ) between harmonics $6 \to 7$ ,
a tone ( $+ 0.31$ ) between harmonics $7 \to 8$ ,
another different tone ( $+ 0.04$ ) between harmonics $8 \to 9$ ,
a triton ( $- 0.17$ ) between harmonics $5 \to 7$ ,
another different triton ( $+ 0.17$ ) between harmonics $7 \to 10$ , etc

These intervals between the harmonics of a given fundamental are called just intervals and will have important roles after.

Ratio of frequencies of just intervals:

In the example above, if

f = f_{C_{3}}

is the frequency of the fundamental, then the frequency of harmonic

4

f_{C_{5}} = 4 f

, and frequency of harmonic

5

f_{E_{5}} = 5 f

. Consequently we get that the ratio of frequencies of the major third just interval

C_{5} \to E_{5}

\frac{f_{E_{5}}}{f_{C_{5}}} = \frac{5 f}{4 f} = \frac{5}{4}

Similarly the ratio of frequencies of the fifth just interval

C_{4} \to G_{4}

\frac{f_{G_{4}}}{f_{C_{4}}} = \frac{3 f}{2 f} = \frac{3}{2}

More generally, there is a just interval between two frequencies

f, f'

if the ratio is

\frac{f'}{f} = \frac{a}{b}

with two small integers

a, b

(say

a, b < 20

Dissonance of a just interval:

We define the dissonance of the just interval

\frac{f'}{f} = \frac{a}{b}

d i s (\frac{a}{b}) : = ln (a b)

for an irreducible fraction

a / b

, and with “

ln

” being the natural logarithm function. (There will be a simpler expression of

d i s (\frac{a}{b})

later).

7.1.4 Just intonation

Just intonation in musics means that the we play music only with just intervals.

We will use two different and complementary representations for the notes constructed with just intervals: the pitch space and the tonnetz space. We will explain after the concept of temperament that explains how we choose 12 (or less) notes per octave.

7.1.5 Equal temperament

In every culture of every time people played with just intonation, i.e. just intervals. The only exception comes from Europe in the mid of XIX-th century, where they introduce the equal temperament, where the octave is divided in logarithmic scale in 12 equal intervals. The consequence is that in the equal temperament, only the octave remains a just interval. The other intervals are not. But the fifth and fourth are very close to just intervals, so that the difference is unperceptive.

Later, we will not consider the equal temperament (except in the pitch space representation, giving some dashed lines of references).

7.2 Tunplot: the pitch space

Watch a video.

The pitch is very well known by musicians, it represents the position of a note on a piano keyboard. Precisely the pitch of a note of frequency

f

is defined by

x = \frac{12}{ln 2} ln (\frac{f}{f_{A_{5}}}) + x_{A_{5}} \in R

where

f_{A_{5}} = 440

Hz is the frequency of the tuning fork and

x_{A_{5}} = 69

is its (MIDI) key number. In other terms

x

represents the position of a note on a MIDI keyboard, where integer values are exactly on the keys (ex:

x = 60

is for

f_{C_{5}}

) but non integer values of

x

are also allowed, between the keys.

For example the pitch of

A_{5}

x_{A_{5}} = 69

and the pitch of

B ♭_{5}

x_{B ♭_{5}} = 70

, hence

x = 69.5

is a pitch at “half-distance” between

A_{5}

and

B ♭_{5}

, sometimes called quarter-tone.

In the program, the representation of the pitch space is called: “tunplot”.

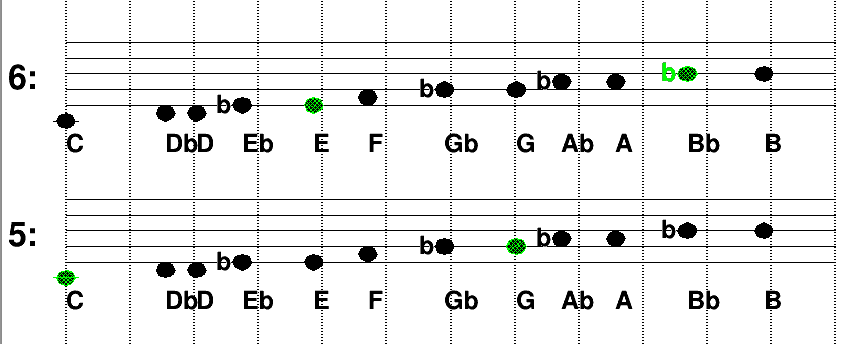
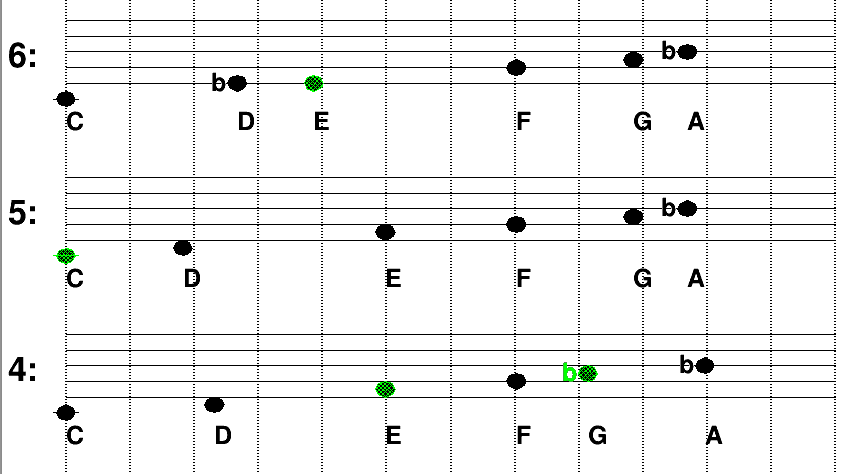
Example 7.1. On the following example, three notes have been played with the keys

F_{4}, C_{5}, E_{5}

. They are represented by the green disks. Their horizontal position gives their pitch

x

, and the dashed lines are is the equal temperament, i.e. for integer value of

x

. (In black are other accessible notes by the temperament, but not yet played).

image: 6_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_1.png

In this example, we observe that

x_{E_{5}}

is a little lower than the equal temperament line. The number on the left of each line is the octave range number.

7.3 Netplot: the tonnetz space

Watch a video.

In German, ton = “note”, netz = “lattice”, so “tonnetz” is the lattice of notes.

Euler in 1750, proposed a tonnetz to represent just intervals, that is a two-dimensional lattice. He used it to represent just intervals with fractions of the form

\frac{a}{b} = 2^{n_{2}} 3^{n_{3}} 5^{n_{5}}

with integers

n_{2}, n_{3}, n_{5} \in Z

. This is not sufficient for our purpose, we will need to use all the prime numbers

{2, 3, 5, 7, 11, 13, \dots}

in our fractions, so we define the tonnetz space as follows: a fraction is written uniquely as

\frac{a}{b} = 2^{n_{2}} 3^{n_{3}} 5^{n_{5}} 7^{n_{7}} \dots

with some integers

n_{2}, n_{3}, n_{5}, n_{7}, \dots \in Z

. We represent

n = (n_{2}, n_{3}, n_{5}, \dots)

as a point in a lattice. In practice we will represent the axis of

n_{3}, n_{5}, n_{7}

, the axis of

n_{11}, n_{13}, n_{17}

are written in small fonts. The value of

n_{2}

(the octave) is not represented, instead we represent the octave position of the note on a circle.

In the program, the representation of the tonnetz space is called: “netplot”.

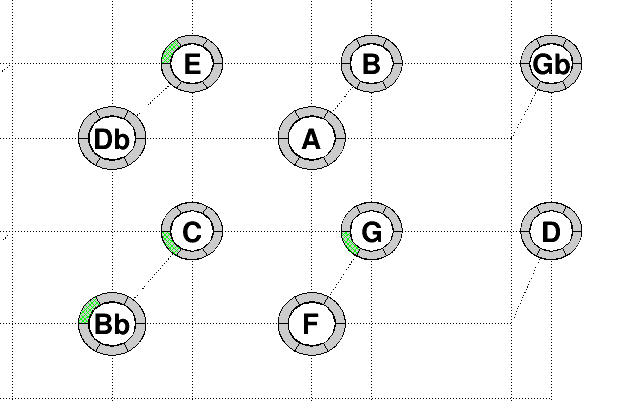
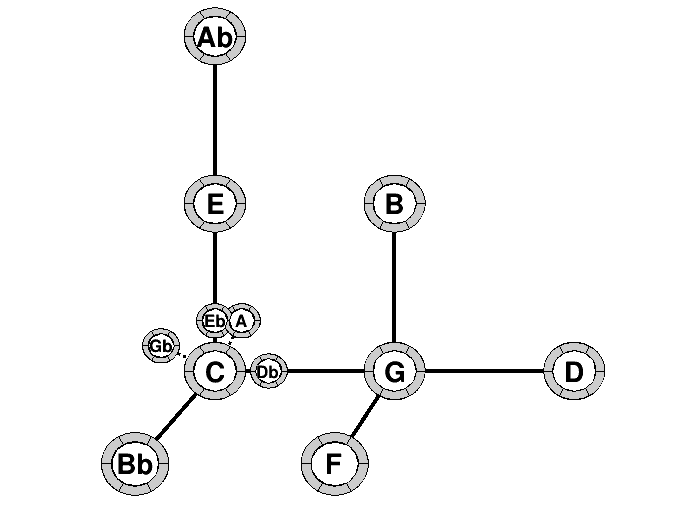
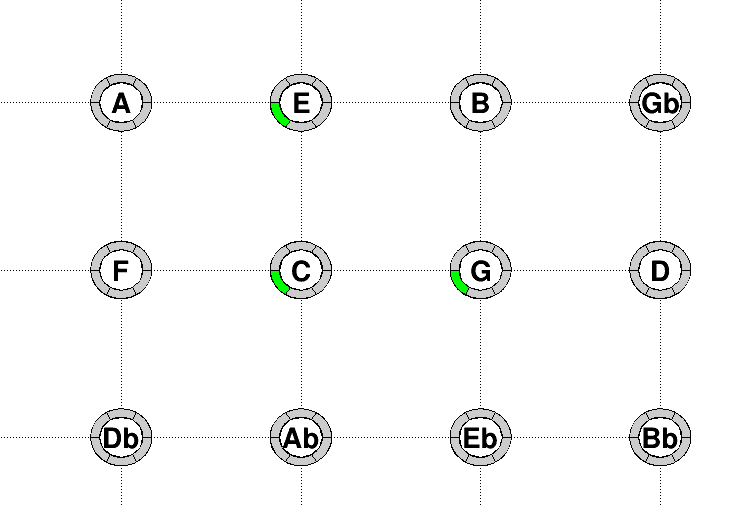
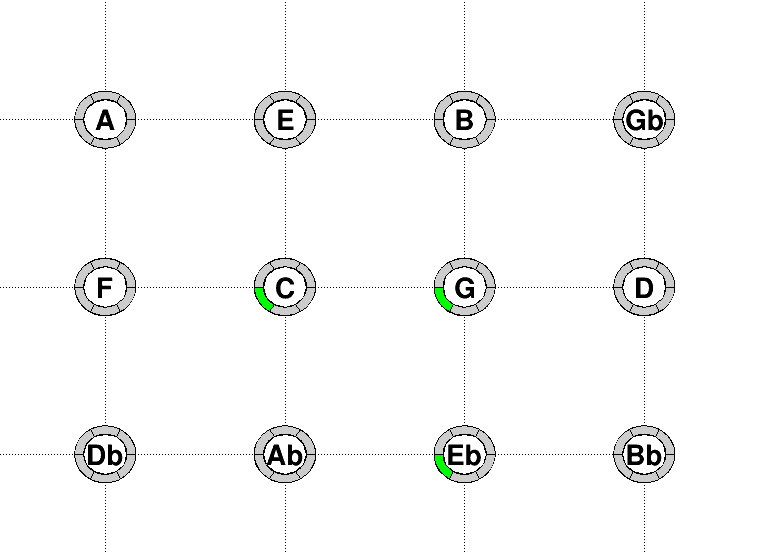
Example 7.2. On the following example (same as 7.1), three notes have been played with the keys

F_{4}, C_{5}, E_{5}

. They are represented by the green domains. (In grey are other accessible notes, but not yet played). The horizontal axis is for

n_{3}

value, the vertical is for

n_{5}

and the octave range value is the position on each circle. From this picture, up to a factor

2

, we can read that the ratio of frequencies are

\frac{f_{C_{5}}}{f_{F_{4}}} = (2^{n_{2}}) 3

and

\frac{f_{E_{5}}}{f_{C_{5}}} = (2^{n'_{2}}) 5

. We also read that

C, E

are in the same octave range

5

and

F

is in the octave range

4

. We can deduce actually that

\frac{f_{C_{5}}}{f_{F_{4}}} = \frac{3}{2}

is a just fifth and

\frac{f_{E_{5}}}{f_{C_{5}}} = \frac{5}{4}

is a just major third. This was not visible from the pitch representation.

image: 7_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_1.png

Summary 7.3. We not need to be a mathematician to read this picture. We only need to observe that the notes

F_{4}, C_{5}

are neighborhoods on the horizontal $n_{3}$ axis which is the axis of just fifths and that

C_{5}, E_{5}

are neighborhoods on the vertical $n_{5}$ axis which is the axis of just major third.

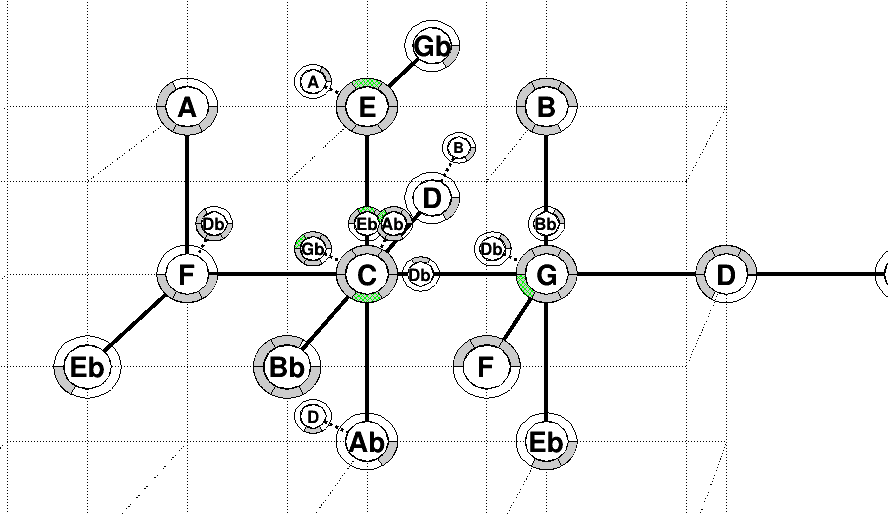
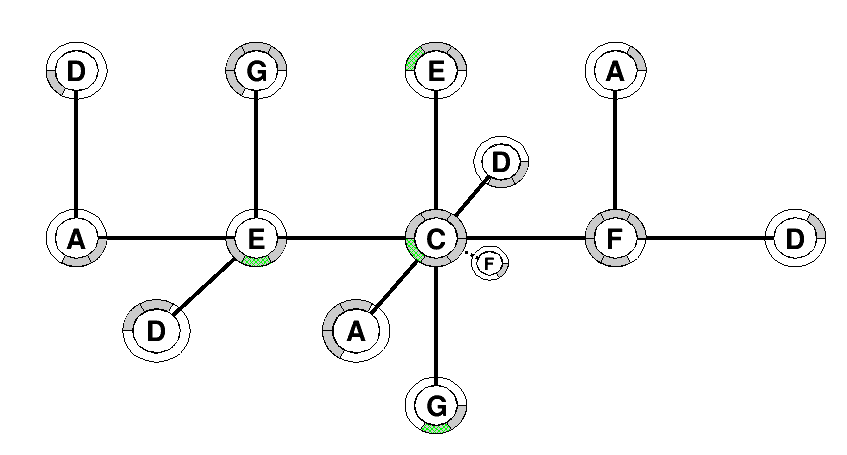
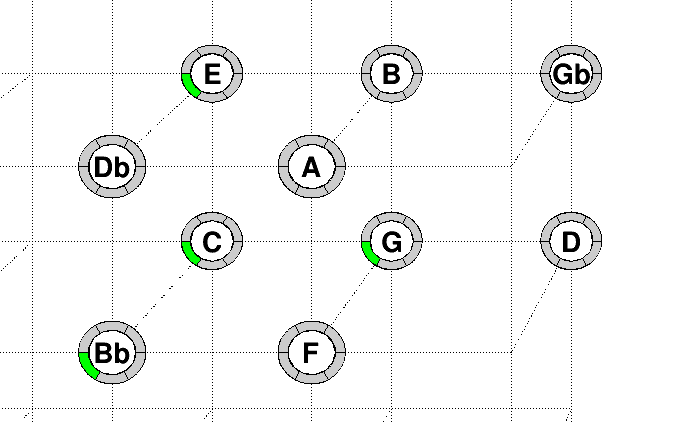
Example 7.4. Here is an example with the three axis

n_{3}, n_{5}, n_{7}

. This is a chord with

C_{5}, G_{5}, E_{6}, B_{6} ♭

. The note

B_{6} b

is along the axis $n_{7}$ which is the axis of just minor seventh.

image: 8_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_2.png

image: 9_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_2.png

Example 7.5. In this more complicated example, we have played the keys

C_{4}, G_{5}, G_{6} ♭, A_{6} ♭, E_{7} ♭, E_{7}

. On the pitch axis, we have added the fractions, where

C_{4}

has the fraction

\frac{1}{1}

, this is the reference note. For example

G_{6} ♭

has the fraction

11 / 2

with respect to

C_{4}

. On the tonnetz it is represented on the axis

n_{11}

, that starts from

C

on the upper-left. Similarly the axis

n_{13}

is on the upper-right, the axis

n_{17}

is on the right, the axis

n_{19}

is above.

image: 10_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_3.png

image: 11_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_3.png

7.4 Formula for pitch values

We have seen of the tunplot figures above that the pitch of notes differs slightly from the equal temperament shown by the vertical dashed lines. Here we explain how to compute the pitch corrections from the position of the note on the tonnetz.

Here is a table

Mathematically the pitch correction

Δ x

for a prime number

p

Δ x = {\frac{12}{ln 2} ln p}

where

{x}

for a given

x \in R

{x} = x + k

with

k \in Z

, such that

{x} \in] - 0.5, 0.5]

. Example,

{\frac{12}{ln 2} ln 3} = 0.01955.. \approx + 0.02

{\frac{12}{ln 2} ln 5} = - 0.136.. \approx - 0.14

etc.

and we explain after how to use it with an example.

Axis	interval	Number of half-tone	pitch correction $Δ x$
		in equal temperament	with respect to equal temperament
$n_{3}$	fifth	$7$	$+ 0.02$
$n_{5}$	major third	$4$	$- 0.14$
$n_{7}$	minor seventh	$10$	$- 0.31$
$n_{11}$	augmented fourth	$6$	$- 0.49$
$n_{13}$	minor sixth	$8$	$+ 0.40$
$n_{17}$	half-tone	$1$	$+ 0.05$
$n_{19}$	minor third	$3$	$- 0.02$

Consider the following example, called harmonic temperament later:

image: 12_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_harm_C.png

image: 13_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_harm_C.png

In this example the reference note is

C

and his pitch is given by the equal temperament, i.e.

x_{C_{5}} = 60.00

. We see on netplot that

E

is a major third from

C

, so

x_{E} = x_{C} + 4 - 0.14

as can been observed on tunplot. Similarly we deduce the following table of pitchs for this “Harmonics scale”

Note	pitch (i.e. half-tones) w.r.t. $C$
$C$	$0$
$D ♭$	$1 + 0.05$
$D$	$2 + 0.02 + 0.02 = 2 + 0.04$
$E ♭$	$3 - 0.02$
$E$	$4 - 0.14$
$F$	$5 + 0.02 - 0.31 = 5 - 0.29$
$G ♭$	$6 - 0.49$
$G$	$7 + 0.02$
$A ♭$	$8 - 0.14 - 0.14 = 8 - 0.28$
$A$	$9 + 0.40$
$B ♭$	$10 - 0.31$
$B$	$11 + 0.02 - 0.14 = 11 - 0.12$

What is important to remember is that:

Intervals along the $n_{3}$ axis, i.e. fifths, do not differ from the equal temperament intervals by a perceptible quantity. And similarly for $n_{17}, n_{19}$ axis.
Intervals along the $n_{5}$ axis of major third get a strong pitch correction $Δ x \approx - 0.14$ (of half-tone) for each positive step.
Intervals along the $n_{7}$ axis of minor seventh get a strong pitch correction $Δ x \approx - 0.31$ (of half-tone) for each positive step.

7.5 Temperaments

There are an infinite number of rational numbers, so in practice if we use an instrument with 12 keys per octaves, we have to choose which frequencies to play. Such a choice of frequency for each key is called a temperament.

7.5.1 Fixed temperament

Watch a video.

If this choice is fixed, we say that we play with a fixed temperament. The program will allow to play with different fixed temperament, like the famous “Pythagorean temperament”, the “Zarlino temperament”, the “Harmonic temperament” etc.. but also on some fixed temperament build by the user. The advantage of fixed temperament is that some fixed “musical mode color” can be explored. The dis-advantage of fixed temperament is that not all the just intervals are available, and some intervals sometimes sound bad.

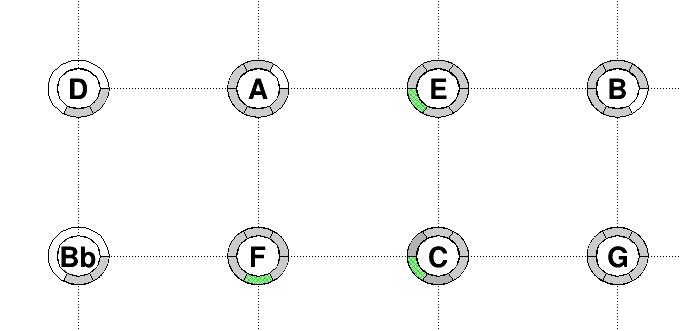
Zarlino temperament in C:

Here is the picture for available notes

image: 14_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_zarlino_C.png

image: 15_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_zarlino_C.png

We observe on the tonnetz space that it is made with just fifths and just major thirds. On the pitch space, we observe that the temperament is the same on each octave range. One advantage of the Zarlino temperament is that we have just major triads chords like

{C, E, G}

{E b, G, B b}

. But beware that some other triads are not the usual just like:

{E, A b, B}

{G b, B b, D b}

Harmonics temperament in C:

Here is the picture for available notes

We observe on the tonnetz space and pitch space that it is made from the first few harmonics of

C

(up to harmonics 25).

7.5.2 Adaptative temperament

Watch video.

Adaptative temperament has been defined and proposed in the paper [1].

Instead of using a fixed temperament, it is also possible to adapt the frequency of some key to the present situation, depending on the notes that are played currently (or recently) and depending on some (deterministic) rules. We say that we play with adaptative temperament. The advantage of adaptative temperament is that all the just intervals may be available. The disadvantage is that the frequency associated to a key may change, and this can be a difficulty to the player. To overcome this difficulty this is very useful for the player to look at the available notes on the tonnetz space and on the pitch space.

Definition of the adaptative temperament:

Suppose that there is already a set of notes, i.e. a chord

A

that sounds. The adaptative temperament depends on this chord

A

. We have to choose how many keys per octave we want to be able to use. This is

N_{o c t} = 4, 6, 12

. Then the octave range is divided in

N_{o c t}

equal intervals and in each of these intervals, we choose the note that is the most consonant with the notes already present in the chord

A

(among the infinity of rational numbers in this interval).

More precisely we use the dissonance function

d_{A} (n)

of a note

n

with respect to the chord

A = {n_{j}, j = 1 \dots N}

made of

N

notes.

d_{A} (n) : = \sum_{j} d (n_{j}, n)

where

d (n_{j}, n) = ln (a b)

is the dissonance of the just interval

\frac{f}{f_{j}} = \frac{a}{b}

made by the pair of notes

n_{j}, n

. (On the tonnetz

d (n_{j}, n)

is just the

L^{1}

distance). The resonance function is just the opposite

R_{A} (n) = - d_{A} (n)

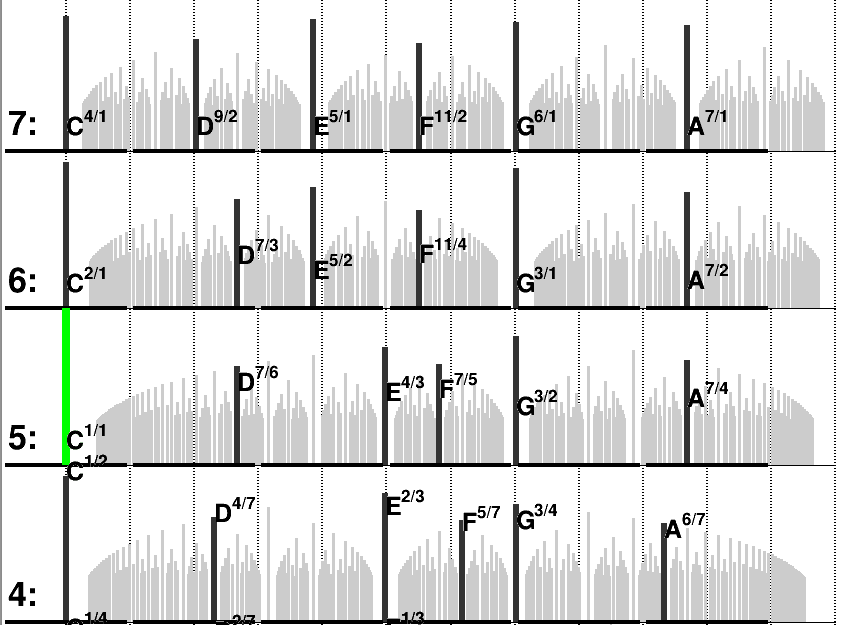
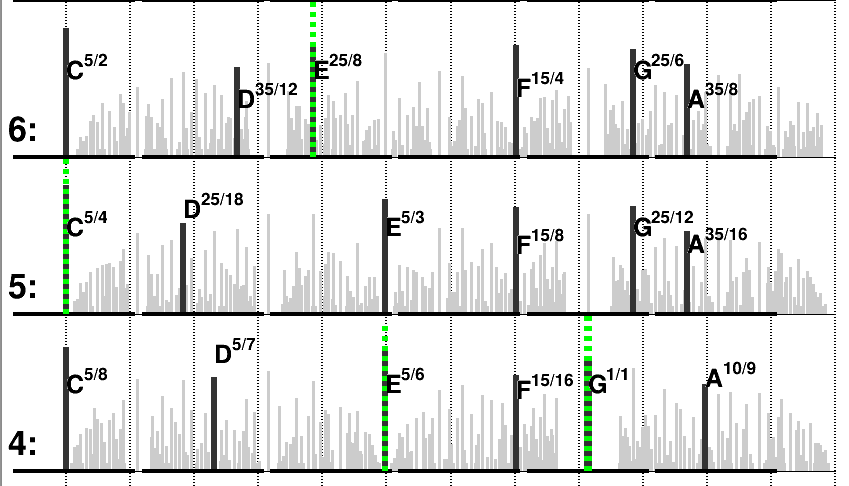
Example 7.6. In this example, the chord is made of the only note

A = {C_{5}}

. We choose

N_{o c t} = 6

notes per octave. For this we are allowed to use only the keys

C, D, E, F, G, A

in each octave. On the first pitch space we represent a vertical bar at (almost) every rational number, i.e. possible new note

n

, and the hight of the bar is the resonance

R_{A} (n) = - d_{A} (n)

. Each octave is decomposed in

N_{o c t} = 6

equal intervals and the black lines is the selection in each interval that gives the highest bar, i.e. the most resonance note, with respect to

A

. This is the adaptative temperament with

N_{o c t} = 6

notes per octave, for the chord

A = {C_{5}}

. The other pictures are as above.

image: 16_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_adapt_C_2.png

image: 17_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_adapt_C.png

image: 18_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_adapt_C.png

Observe that the temperament is not the same at each octave. We observe interestingly that the scale in octave

5

is the “blues scale”.

Example 7.7. In this example, the chord is made of four notes

A = {E_{4}, G_{4}, C_{5}, E_{6}}

. We choose

N_{o c t} = 6

notes per octave.

image: 19_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_adapt_chord.png

image: 20_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_tonnetz_adapt_chord.png

image: 21_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_pitch_adapt_chord_2.png

We observe that the adaptative temperament depends indeed on the chord

A

8 Some examples of just intervals, just chords and chord progressions

By definition of just chord is a set of notes such that each interval is a just interval. Hence a just chord is a set of notes displayed on the tonnetz.

For example a major triad is displayed as a triangle on the

n_{3}, n_{5}

axis with a right angle at the bottom left. Here is

{C, E, G}

image: 22_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_major_triad.png

For example a minor triad is displayed as a triangle on the

n_{3}, n_{5}

axis with a right angle at the top right. Here is

{C, E b, G}

image: 23_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_minor_triad.png

For example a dominant seventh chord is displayed as a tetrahedron on the

n_{3}, n_{5}, n_{7}

axis. Here is

{C, E, G, B b}

image: 24_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_chord_CEGBb.png

In Section 7.1.2, we have seen there are different just minor thirds between harmonics

5 - 6

and

6 - 7

. Correspondingly there are different minor seventh chords. For example here is a first

{C, E b, G, B b}

image: 25_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_chord_CEbGBb_1.png

Here is a second non-equivalent

{C, E b, G, B b}

image: 26_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_chord_CEbGBb_2.png

Observations: the first

{C, E b, G, B b}

is composed of fifths and thirds. The second

{C, E b, G, B b}

is composed of fifths and minor sevenths. They sound very different (see the video).

8.1 Great cadence

See Video.

9 Advanced use of the plugin

9.1 Automation

Automation means that some parameter of the plugin can be recorded on a MIDI track and play after. For example a parameter can be the choice of 'temperament'.

This allows that a parameter evolves during the reading of a MIDI track.

9.2 Adaptative temperament with different N_keys and levels

Choose adaptative temperament with 4 keys/octave
Choose adaptative temperament with 6 keys/octave
Choose adaptative temperament with 3/6/12
- In octave 4, put hold notes in leader mode: C,Ab,E, this play a minor triad. Then play in follower mode, not hold, in higher octaves.

9.3 Many musicians, how to use in session

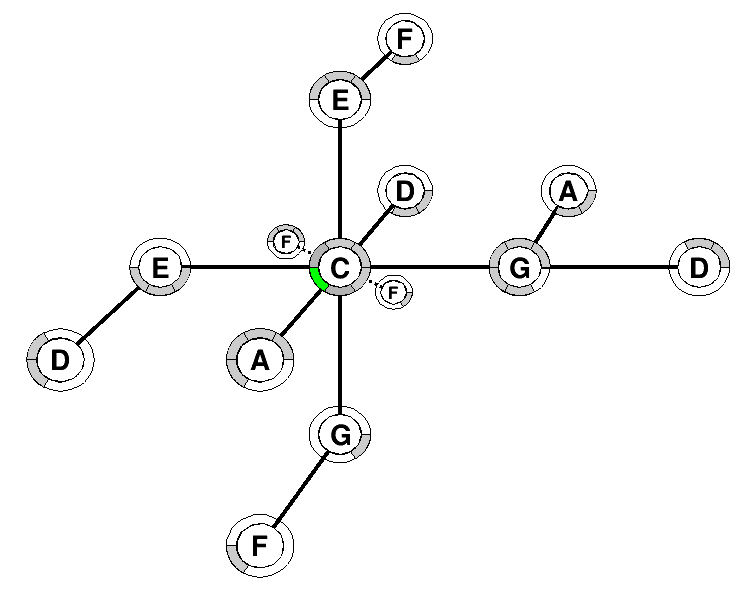
We propose here a setup how to use the plugin(s) in a session with many musicians (here Bo and Malik).

We propose as seen on the picture below,

On input there are audio (in green) and midi (in red) signals. Each input is connected to an individual midi track with a tonnetz plugin. In fact all the plugins communicate in the computer and share the same list of notes and the same tonnetz space. Beware that a plugin VST3 can not communicate with a AU plugin, so all the plugins should be of the same type VST3 or AU.
On output of the plugin we can choose to use the internal synthetizer (IS) of Alex that gives an audio output. This audio output is then sent to a mixer table.
On output of the plugin we can choose not to use the internal synthetizer of Alex but send the midi signal to an external synthe, and after the audio signal to the mixer table.
The musicians have a direct access to the plugin parameters through a computer console. They can also send automatic commands to the plugin using a Foot-Pad midi controller. The commands can be assigned from the computer console.
In practice the developpers can have also an access to the computer from an external computer, using “AnyDesk”.

image: 27_home_faure_c++_musique_JUCE_fred_Tonnetz_doc_figures_system2.png

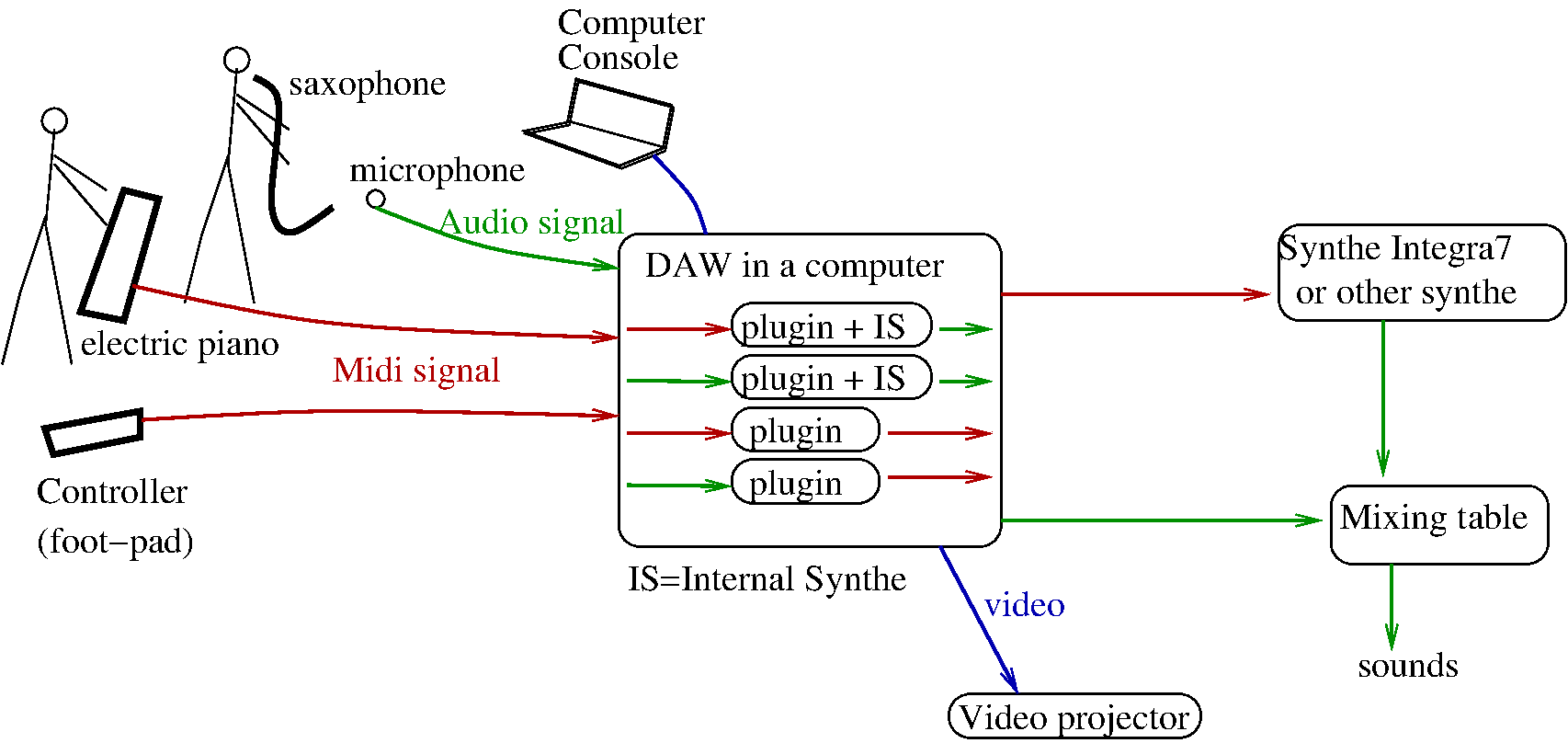
Details on midi connections:

if the controleur uses a DIN connection, one has to use either a convertissor or the midibox.

A EWI

A.1 EWI USB

web page

A.2 EWI 5000

Ewi 5000 is a MIDI saxophone.

Manual

A.2.1 Configuration with the software EWI5000

set Key delay = 2. (not more not less)
Fingering: EWI

A.2.2 Configuration (once for ever)

The program tonnetz uses bite events from EWI5000. You have to configure the EWI5000 as follows, (see page 17,18 of the manual for details)

Configure the bite sensor:
1. No Filter, No Pitch bend, no Breath sensor
2. But CC enabled: En with a dot, Cn is 20 (= x14), nb is 0 and bt is 27.
As a result, the bite event will send a midi message: $0 x B 0 + c h, 0 x 14, v$ where $0 \leq v \leq 127$ is the value.

A.2.3 Midi messages

EWI5000 sends the following messages (given here in hexa):

Note on $90 + c h, k e y, v e l$
Note off: $80 + c h, k e y, v e l$
Breath control fine, coarse:
Controller Potamento, on/off and coarse:
PitchWheel:
Bite event: $B 0 + c h, 14, v$ where $14$ is setup as explained above.

References

1F Faure, M. Mezzadri, and F. Ratchov, "Analyse et jeu musical en tempérament juste adaptatif", https://hal.archives-ouvertes.fr/hal-01119499link (2015).

«Harmonics» project

Table of Contents

Documents and references:

1 Installation of plugin Tonnetz and softwares on the computer Mac-Os

2 How to use

2.1 Program Tonnetz (StandAlone)

3 Versions and news

21/01/2024, version 1.1.1

19/02/2024, version 1.1.9

19/02/2024, version 1.1.10

20/04/2024, version 1.1.12

23/05/2024, version 1.1.13

21/07/2024, version 1.1.16

4 Sessions passées

5 Objectives of the project

5.1 First ojectives

5.1.1 For Alex & Fred

5.1.2 For Bo & Malik

5.1.3 Together (Alex, Bo, Fred, Malik)

5.2 Some conferences?

Une conférence sur les tempéraments anciens et actuels?

5.3 Objectives

6 Pedagogical tutorial: «how to start with the plugin tonnetz»

6.1 Summary of the tonnetz plugin with few key-words

6.1.1 MIDI,Audio, DAW and plugins

6.1.2 The tonnetz

7 Theoretical description

7.1 Harmonics and just intervals

7.1.1 Human voice and importance of harmonics and just intervals

Auditive illusion:

7.1.2 What are the harmonics

Frequency of the harmonics:

7.1.3 What are just intervals

Ratio of frequencies of just intervals:

Dissonance of a just interval:

7.1.4 Just intonation

7.1.5 Equal temperament

7.2 Tunplot: the pitch space

7.3 Netplot: the tonnetz space

7.4 Formula for pitch values

7.5 Temperaments

7.5.1 Fixed temperament

Zarlino temperament in C:

Harmonics temperament in C:

7.5.2 Adaptative temperament

Definition of the adaptative temperament:

8 Some examples of just intervals, just chords and chord progressions

8.1 Great cadence

9 Advanced use of the plugin

9.1 Automation

9.2 Adaptative temperament with different N_keys and levels

9.3 Many musicians, how to use in session

Details on midi connections:

A EWI

A.1 EWI USB

A.2 EWI 5000

A.2.1 Configuration with the software EWI5000

A.2.2 Configuration (once for ever)

A.2.3 Midi messages

References