Chapitre 2  Étude de fonctions

2.1  Exercice : étude de f(x)=2x²−1/6x²+x−2

1. Domaine de définition
   On tape :
   solve(6x^2+x-2)
   On obtient :
   [(-2)/3,1/2]
   Donc f est définie sur ℝ−{−2/3,1/2}
2. Dérivée
   On tape :
   factor(diff((2x^2-1)/(6x^2+x-2))
   On obtient :
   (2*x^+4*x+1)/((2*x-1)^2*(3*x+2)^2)
   On tape :
   normal(solve(2*x^+4*x+1))
   On obtient :
   [(-sqrt(2)-2)/2,(sqrt(2)-2)/2]
   On tape :
   evalf([(-sqrt(2)-2)/2,(sqrt(2)-2)/2])
   On obtient :
   [-1.70710678119,-0.292893218813]
   On tape :
   subst((2x^2-1)/(6x^2+x-2),x=-1.70710678119)
   On obtient :
   0.35044026276
   On tape :
   subst((2x^2-1)/(6x^2+x-2),x=-0.292893218813)
   On obtient :
   0.465886267852
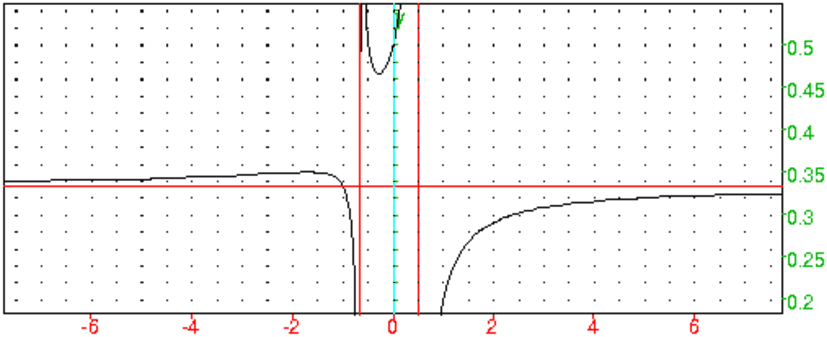
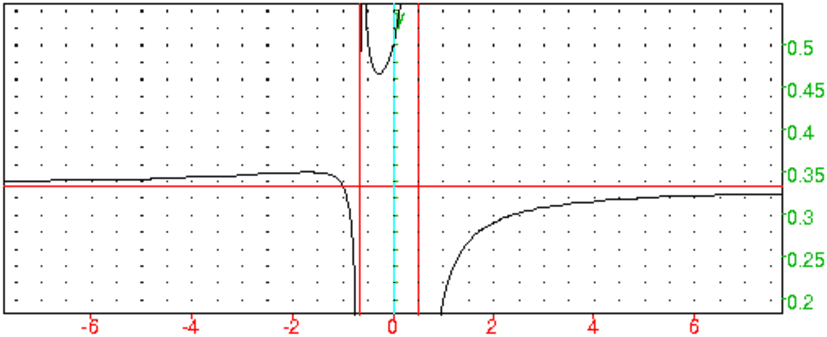
   f a donc deux extremum en ≃ (-1.71,0.35) et (-0.29,0.47)
   Donc f est :
   croissante sur ]−∞;(−√2−2)/2]
   décroissante sur [(−√2−2)/2; −2/3[
   décroissante sur ]−2/3;(√2−2)/2]
   croissante sur [(√2−2)/;1/2[
   croissante sur ]1/2;+∞[
3. Branches infinies
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=inf)
   On obtient :
   1/3
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=-inf)
   On obtient :
   1/3
   Donc y=1/3 est asymptote.
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=-2/3,-1)
   On obtient :
   -infinity
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=-2/3,1)
   On obtient :
   +(infinity)
   Donc x=−2/3 est asymptote.
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=1/2,-1)
   On obtient :
   +infinity
   On tape :
   limit((2x^2-1)/(6x^2+x-2),x=1/2,1)
   On obtient :
   -infinity
   Donc x=1/2 est asymptote.
4. Graphe
   On tape :
   plotfunc((2x^2-1)/(6x^2+x-2),x=-8..8),
   affichage(droite(x=1/2),droite(x=-2/3),droite(y=1/3),1)
   On obtient :
   

2.2  Exercice : étude de f(x)=  acos (sin(x))+  asin (cos(x))

1. Domaine de définition et période.
   
2. Montrer que :
   f(x+π)=f(π/2−x)=π−f(x).
3. Graphe de f et préciser son centre de symétrie et son axe de symétrie.
4. Valeur de f(x) sur [0,π/2] et sur π/2,π].

Rappels
On a :
sin(x)=cos(π/2−x)
cos(x)=sin(π/2−x)
sin(x+π)=−sin(x)
cos(x+pi)=−cos(x)
  asin (x) est une bijection de [-1,1] sur [−π/2,π/2] sin(  asin (x))=x et
si x∈ [−π/2,π/2] alors   asin (sin(x))=x
  acos (x) est une bijection de [-1,1] sur [0,π] cos(  acos (x))=x et
si x∈ [0,π] alors   acos (cos(x))=x
  asin (−x)=−  asin (x)
  acos (−x)=π−  acos (x)
  asin (x)+  acos (x)=π/2
  asin (x)′=1/√(1−x²)
  acos (x)′=−1/√(1−x²)
La solution avec Xcas On tape :
f(x):=acos(sin(x))+asin(cos(x))
donc
f(x):=acos(cos(pi/2-x))+asin(sin(pi/2-x))

1. f(x+π)=f(π/2−x)=π−f(x).
   On tape :
   simplify(f(x+pi)+f(x))
   On obtient :
   pi
   En effet :
   f(x+pi)=acos(-sin(x))+asin(-cos(x))
   et on a :
     acos (−sin(x))=π−  acos (sin(x))
     asin (−cos(x))=−  asin (cos(x))
   D’où le rèsultat.
   On tape :
   simplify(f(pi/2-x)+f(x))
   On obtient :
   pi
   En effet :
   f(pi/2-x)=acos(cos(x))+asin(sin(x))
   et on a :
     acos (sin(x))+  asin (sin(x)=π/2
     asin (cos(x))+  acos (cos(x))=π/2
   D’où le rèsultat.
2. Graphe de f.
   On tape :
   f(x):=acos(sin(x))+asin(cos(x))
   plotfunc(f(x))
   On obtient :
   Le point S(π/4,π/2 est un centre de symétrie car on a f(x)+f(pi/2−x)=π donc les points A(x,f(x) et B(π/2−x,f(π/2−x) sont 2 points de la courbe qui sont symétriques par rapport à S.
   En effet 1/2*(x+π/2−x)=π/4 et 1/2*(f(x)+f(π/2−x))=π/2.
   La droite d’équation x=3π/4 est un axe de symétrie de la courbe.
   En effet f(x+π)=f(π/2−x) et donc les points C(x+π,f(x+π) et D(π/2−x,f(π/2−x) sont symétriques par rapport à la droite x=3π/4 puisque 1/2*(x+π+π/2−x)=3π/4
3. Valeur de f(x) sur [0,π/2] et sur π/2,π]. On tape :
   assume(x>0 and x<pi/2)
   simplify(f(x))
   On obtient :
   pi-2*x
   Si x∈ [0,π/2] on a π/2−x∈ [0,π/2] donc f(x):=  acos (cos(π/2−x))+  asin (sin(π/2−x))=π−2x On tape :
   assume(x>=pi/2 and x<=pi)
   simplify(f(x))
   On obtient :
   0
   Si x∈ [π/2,π] on a x−π/2∈ [0,π/2] donc f(x):=  acos (cos(π/2−x))+  asin (sin(π/2−x))=
     acos (cos(x−π/2))−  asin (sin(x−π/2−))=x−π/2−(x−π/2)=0