


suivant: Méthode numériques (itératives)
monter: Réduction exacte des endomorphismes
précédent: Calcul du polynôme minimal
Recherche de vecteurs propres
On suppose que le polynôme minimal PA est sans facteur carré
(square-free) ce qui se vérifie en cherchant le pgcd
de PA avec sa dérivée (sinon A n'est pas diagonalisable).
À l'aide du polynôme minimal, il est facile de déterminer les
vecteurs propres de A correspondant aux racines de PA que l'on
sait déterminer car si
PA(X) = (X - 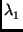 )×Q(X) on a :
)×Q(X) on a :
Im
Q(
A) = Ker (
A -
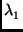 I
I)
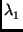 I)×Q(A) = PA(A) = 0 on a :
I)×Q(A) = PA(A) = 0 on a :
Im
Q(
A)
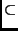
Ker (
A -
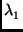 I
I)
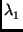 ) et Q(X) sont premiers entre eux car PA est sans facteur carré donc d'après Bézout,
il existe deux polynômes U et V tels que :
) et Q(X) sont premiers entre eux car PA est sans facteur carré donc d'après Bézout,
il existe deux polynômes U et V tels que :
U(
X)×(
X -
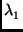
) +
Q(
X)×
V(
X) = 1
on a donc :
U(
A)×(
A -
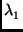 I
I) +
Q(
A)×
V(
A) =
I
Si
x 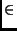 Ker (A -
Ker (A - 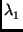 I), alors
I), alors
U(
A)×(
A -
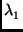 I
I)
x +
Q(
A)×
V(
A)
x =
x
donc :
Q(A)(V(A)x) = x
d'où :
Im
Q(
A)
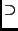
Ker (
A -
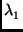 I
I)
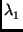 I)p1 lorsque
I)p1 lorsque 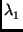 est
d'ordre p1).
est
d'ordre p1).
Exercice 3 (à rendre au début du TP6)
Trouver une base de vecteurs propres de la matrice B de l'exercice 1
en utilisant la méthode ci-dessus.



suivant: Méthode numériques (itératives)
monter: Réduction exacte des endomorphismes
précédent: Calcul du polynôme minimal
Bernard Parisse
2004-06-04