Calcul du polynôme minimal (méthode déterministe)

On considère d'abord A comme un vecteur de l'espace des matrices ayant n² coordonnées (par exemple la matrice identité en dimension 2 a pour coordonnées (1,0,0,1)) et on va chercher par la méthode du pivot de Gauß une relation non triviale entre les puissances successives de A (on peut se limiter à I, A, .., Aⁿ car le polynôme caractéristique de A annule A).

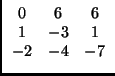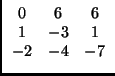
Exercice 1 (à rendre à la fin du TP5)
Générez une matrice carrée aléatoire de taille 3, qu'on notera A. Calculez avec un logiciel A², A³. Créez une matrice avec 4 lignes et 10 colonnes, chaque ligne contiendra les 9 coordonnées de respectivement I, A, A², A³ et en dernière colonne 1, x, x², x³.
On va appliquer la méthode du pivot de Gauß pour réduire cette matrice sous forme échelonnée, mais comme on est intéressé par la relation faisant intervenir des termes de plus bas degré possible, l'ordre des lignes de la matrice à réduire par le pivot de Gauß doit être préservé : si on tombe sur un pivot nul, on ne fera pas un échange de lignes mais on échangera la colonne avec une des colonnes suivantes dont le coefficient sur la ligne du pivot est non nul (ceci correspond à changer l'ordre dans lequel on écrit les coordonnees de I, A, etc.). Si la ligne du pivot est nulle, on obtient alors le polynôme minimal.
Déterminer par cette méthode le polynôme minimal de A et de la matrice :

B = $$\left(\vphantom{\begin{array}{ccc} 0 & 6 & 6 \\ 1 & -3 & 1 \\ -2 & -4 & -7 \end{array}}\right.$$$$\begin{array}{ccc} 0 & 6 & 6 \\ 1 & -3 & 1 \\ -2 & -4 & -7 \end{array}$$$$\left.\vphantom{\begin{array}{ccc} 0 & 6 & 6 \\ 1 & -3 & 1 \\ -2 & -4 & -7 \end{array}}\right)$$