


suivant: À propos de ce
monter: Méthode numériques (itératives)
précédent: Méthode de la puissance.
La méthode des itérations inverses consiste lorsque l'endomorphisme f
est inversible à appliquer l'algorithme de la puissance à f-1
en effet:
si 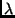 est une valeur propre de f et si w est un vecteur propre
associé à
est une valeur propre de f et si w est un vecteur propre
associé à 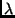 on a :
on a :
f (w) = 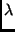 w
w 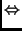 f-1w =
f-1w = 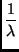 w
w
La méthode des itérations inverses permet donc de trouver la valeur
propre de plus petit module (à condition d'avoir inversé la matrice
A associée à f).
La méthode des itérations inverses est utile
lorsqu'on connait une valeur approchée 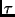 d'une valeur propre
d'une valeur propre
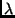 .
On peut alors améliorer
.
On peut alors améliorer 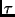 en utilisant des itérations inverses,
puisqu'alors la matice
B = A -
en utilisant des itérations inverses,
puisqu'alors la matice
B = A - 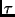 I est inversible et possède
I est inversible et possède
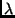 -
- 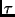 (qui est très petit) comme valeur propre.
(qui est très petit) comme valeur propre.
On cherche l'inverse de
B = A - 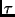 I,
puis on pose :
I,
puis on pose :
y0 = B-1b où b est un vecteur aléatoire (y0 est alors
proche d'un vecteur propre correspondant à
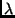
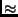
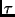 .
.
On itère ensuite la procédure.
Exercice 5 (à rendre à la fin du TP6)
Trouvez la valeur propre la plus proche de -3.5 des matrices de l'exercice 4.



suivant: À propos de ce
monter: Méthode numériques (itératives)
précédent: Méthode de la puissance.
Bernard Parisse
2004-06-04