


Next: Noyau et vecteurs isotropes
Up: miasquad
Previous: miasquad
Exercice Q1 (à rendre fin de la séance 2)
Écrire une fonction qui vérifie qu'une fonction de plusieurs variables
est une forme quadratique et renvoie alors sa matrice ou renvoie
0 sinon.
Les paramètres de la fonction seront
l'expression q de la forme quadratique et la liste x
des variables (par exemple
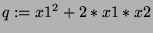 ; x:=[x1,x2];).
; x:=[x1,x2];).
Indication:
On remarquera qu'une expression est quadratique en x:=[x1,...,xn];
si elle vaut zéro en  , si sa différentielle vaut zéro en
, si sa différentielle vaut zéro en
 et si les dérivées partielles d'ordre 2 sont des constantes
(i.e. les dérivées partielles d'ordre 3 sont nulles)
et si les dérivées partielles d'ordre 2 sont des constantes
(i.e. les dérivées partielles d'ordre 3 sont nulles)
Rappels :
- La fonction subs(q,x[i]=0) (MuPAD) ou subs(x[i]=0,q)
(maple) permet de remplacer xi par 0 dans q.
- La fonction diff(q,x[i]) permet de dériver q par
rapport à xi.
Application: exercice Q2 (à rendre fin de la séance 2)
On considère dans 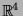 la forme quadratique :
la forme quadratique :
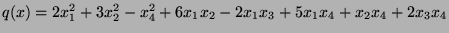
Écrire la forme bilinéaire symétrique 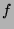 forme polaire de
forme polaire de 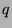 .
.
Écrire la matrice associée à 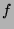 dans la base canonique.
dans la base canonique.
Tester votre fonction avec 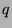 ,
, 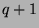 et
et 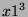 .
.



Next: Noyau et vecteurs isotropes
Up: miasquad
Previous: miasquad
2003-02-19
![]() la forme quadratique :
la forme quadratique :
![]()
![]() forme polaire de
forme polaire de ![]() .
.
![]() dans la base canonique.
dans la base canonique.
![]() ,
, ![]() et
et ![]() .
.