, on prolonge bien sur par
. Il suffit donc de comprendre la transformation
associée à une translation uniforme de vitesse v.
On commence par normaliser le temps en le multipliant par c pour
des raisons d'homogénéité. Notre transformation doit être
linéaire, on la représente donc par une matrice M 
. Sans
restreindre la généralité, on peut supposer que v est dans la
première direction. On peut décomposer l'espace-temps en
deux sous-espaces de dimension 2: le premier contient le temps et la
direction de déplacement, le deuxième les 2 directions spatiales
orthogonales. Ces deux sous-espaces sont conservés par M.
Dans le premier sous-espace ((x,t)), les vecteurs (1,1) et (-1,1)
sont vecteurs propre (puisque la vitesse de la lumière
est constante) de valeurs propres respectives 
et 
(qui dépendent de la vitesse v).
Enfin, changer v en -v revient à changer le sens du temps
((1,1) devient -(-1,1)), donc 
.
La matrice de la transformation restreinte à (x,t) s'écrit:
Revenons à la base canonique, on a:
D'où:
On remarque que l'origine du repère en translation se déplace à la vitesse v dans le repère de départ et 0 dans son propre repère donc:
d'où:
Comme:
on en déduit que la vitesse du premier repère dans le repère en translation est -v. Ce qui signifie que l'inverse de M est la matrice correspondant à la vitesse de translation -v. Donc
.
On peut maintenant déterminer à l'aide de (2)
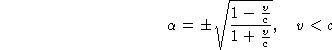
et:
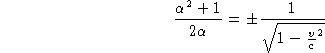
Il faut choisir le signe + sous peine de changer l'orientation en temps.
Pour les directions y et z, que la vitesse soit v ou -v ne change rien donc la valeur propre correspondante est égale à son inverse, comme elle vaut 1 pour v=0, les valeurs propres selon y et z valent 1 par continuité. On obtient ainsi:
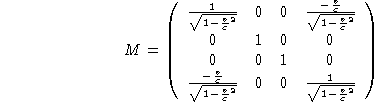
Enfin, on vérifie que la vitesse de la lumière est conservée dans toutes les directions. On montre en fait que la forme quadratique q(dx1,dx2,dx3,c dt)=c2 dt2-dx12-dx22-dx32 est conservée par M:
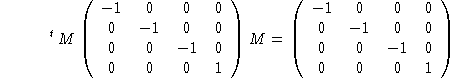
Comme les trajectoires de vitesse c ont un vecteur directeur dans le noyau de q elles conservent leur vitesse après tranformation.
