Elimination des valeurs propres trouvées

Si la matrice A est symétrique, et si e_n est un vecteur propre normé écrit en colonne, on peut considérer la matrice B = A - x_ne_ne_n^t qui possède les mêmes valeurs propres et mêmes vecteurs propres que A avec même multiplicité, sauf x_n qui est remplacé par 0. En effet les espaces propres de A sont orthogonaux entre eux, donc

Be_n = x_ne_n - x_ne_ne_n^te_n = 0, Be_k = x_ke_k - x_ne_ne_n^te_k = x_ke_k

On peut donc calculer la 2ème valeur propre (en valeur absolue), l'éliminer et ainsi de suite.

Si la matrice A n'est pas symétrique, on peut utiliser une technique analogue lorsque 0 n'est pas valeur propre de A (on peut s'y ramener en ajoutant à A un multiple de l'identité). En effet on peut construire un vecteur propre de B pour une valeur propre x_k 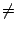$\neq$ 0 à partir d'un vecteur propre de B, en cherchant y tel que tel que

B(e_k - ye_n) = x_k(e_k - ye_n)

On obtient pour le membre de gauche :

Be_k - yBe_n = Be_k = (A - x_ne_ne_n^t)e_k = x_ke_k - x_ne_n.e_ke_n

et pour le membre de droite

x_ke_k - yx_ke_n

d'où l'équation

yx_k = x_ne_n.e_k

Néanmoins cette méthode n'est pas stable, en particulier si la valeur propre e_k est proche de 0, car les vecteurs propres se rapprochent alors tous de e_n.