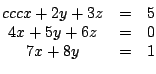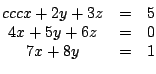


suivant: Inverse
monter: Applications de Gauss
précédent: Déterminant
Index
Réduction sous forme échelonnée (rref)
On réduit la matrice puis on divise chaque ligne par son premier
coefficient non nul. Si la matrice représentait un système
linéaire inversible on obtient la matrice identité sur les colonnes
sauf la dernière et la solution en lisant la dernière colonne.
La relation conservée est en effet Ax = b où x est la solution
de l'équation, et à la fin de la réduction A = I.
Par exemple pour résoudre le système
on réduit sous forme échelonnée la matrice
[[1,2,3,5],[4,5,6,0],[7,8,0,1]], ce qui donne
[[1,0,0,-9],[0,1,0,8],[0,0,1,-2/3]], d'où la solution
x = - 9, y = 8, z = - 2/3.
Retour à la page principale de mat249