


suivant: Résolutions d'équations
monter: Aperçu des possibilités des
précédent: Dérivée, intégrale
On tape, pour avoir le graphe de l'expression f :
On tape, pour avoir le graphe de la fonction g :
On obtient le graphe de la courbe d'équation
y = (2x + 1)/(x2 + 1).
Pour tracer la tangente en un point d'abscisse 0, on tape :
On tape, pour avoir l'équation de la tangente au graphe de la fonction sin(x) au point d'abscisse
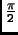 :
On obtient :
Pour tracer une famille paramétrée de fonctions, on peut utiliser
$, par exemple :
:
On obtient :
Pour tracer une famille paramétrée de fonctions, on peut utiliser
$, par exemple :
On tape, pour avoir le tracé de la surface z = x2 - y2 :
On obtient une surface en dimension 3.
Documentation de giac écrite par Renée De Graeve