Retour à la page personnelle de Bernard Parisse.Chapitre 4 Arithmétique en terminale scientifique
4.1 Énoncé sur la partie entière
Montrer que la partie entière de a=(3+√5)n est un entier impair
quelque soit l’entier n dans ℕ.
4.1.1 Cherchons avec Xcas
On peut faire des essais dans le tableur.
Dans A0 on met 1
Dans A1 on met =A0*(3+sqrt(5))
Dans B0 on met =floor(A0)
Dans B1 on met =floor(B1)
Puis on remplit vers le bas.
Dans cet exercice il faut penser à associer à
(3+√5)n sa quantité conjuguée (3−√5)n.
Dans C0 on met 1
Dans C1 on met =C0*(3-sqrt(5))
Dans D0 on met =floor(A0+C0)
Dans D1 on met =C0*(3-sqrt(5))
Puis on remplit vers le bas.
4.1.2 La démonstration
On remarque que :
b=(3+√5)n+(3−√5)n est un entier pair (d’après la formule du
binôme) et que 0<(3−√5)n<1.
On a donc a<b<a+1, ou encore b−1<a<b avec b un entier pair.
Cela prouve que la partie entière de a=(3+√5)n est b−1
qui est un entier impair.
4.2 Énoncés sur le nombre de diviseurs d’un entier
4.2.1 L’énoncé 1
Quel est, parmi les entiers naturels de 1 à 2005, celui qui admet le plus
de diviseurs ? Quel est ce nombre de diviseurs ?
4.2.2 Réponse avec Xcas
On tape :
2*3*5*7
On obtient :
210
On tape :
2*3*5*7*11
On obtient :
2310
Cela nous dit que le nombre est de la forme :
2a*3b*5c*7d avec a ≥ b ≥ c ≥ d ≥ 0
et alors son nombre de diviseurs est :
(a+1)(b+1)(c+1)(d+1)
On peut maintenant faire une recherche systématique :
Il semble qu’il faut supposer que d ≠ 0 car avec
- b=0,c=0, d=0 on ne peut avoir que 210 qui n’a que 11 diviseurs,
- c=0,d=0 (a+1)(b+1)
vaut 20 pour a=9 et b=1 (29*3=1536)
vaut 28 pour a=6 et b=3 (26*33=1728)
- d=0 (a+1)(b+1)(c+1)
vaut 32 pour a=7, b=1 et c=1 (27*3*5=1920)
vaut 36 pour a=5, b=2 et c=1 (25*32*5=1444)
- si d ≠ 0
On tape :
210*6
On obtient :
1260
et 1260 admet 3*3*2*2=36 diviseurs ou on tape :
size(idivis(1260))
On obtient :
36
On tape :
210*8
On obtient :
1680
et 1680 admet 5*2*2*2=40 diviseurs ou on tape :
size(idivis(1680))
On obtient :
40
On fait une recherche systématique :
210=1024 a 11 diviseurs,
29*3=1536 a 20 diviseurs,
27*32=1116 a 24 diviseurs,
26*33=1728 a 28 diviseurs,
24*34=1296 a 25 diviseurs,
27*3*5=1920 a 32 diviseurs,
25*32*5=1440 a 24 diviseurs,
24*3*5*7=1680 a 40 diviseurs.
4.2.3 L’énoncé 2
1/ Trouver le plus petit nombre entier n qui admet exactement 50
diviseurs.
2/ Existe-t-il un entier m qui soit inférieur à n et qui admette plus
de 50 diviseurs ?
4.2.4 Réponse avec Xcas
On sait que si n=ap*bq*cr le nombre de diviseurs de n est
(p+1)(q+1)(r+1).
On a :
50=1*50=2*25=10*5=2*5*5
1/ On cherche le plus petit nombre entier qui admet exactement 50 diviseurs,
donc les candidats sont :
249
224*3
29*34
24*34*5
C’est donc 6480=24*34*5
On tape :
size(idivis(6480))
On obtient :
50
2/ On doit avoir :
m<24*34*5 donc pour qu’il est plus que 50 diviseurs il faut que m soit de
la forme m=2p*3q*5r*7s avec p<=4,q<4,r=1,s=1 et 4(p+1)(q+1)>50.
Essayons p=4,q=2, on a 4(p+1)(q+1)=60>50 et m=24*32*5*7=5040.
Donc m= répond à la question.
4.2.5 L’énoncé 3
Soit une séquence L d’objets. On prend 3 objets parmi cette séquence
L. Écrire un programme triplets qui renvoie la séquence de
dimension comb(size(L),3) constituée par les 3 objets obtenus.
Application numérique
L est la liste des diviseurs de n=12.
Soit un entier n. On cherche 3 diviseurs différents n1,n2,n3 de
n, tels que n1+n2+n3 soit aussi un diviseur de n.
Modifier le programme précédent en solutions pour obtenir toutes les
solutions.
Application numérique
n=12
n=60
n=6279
On tape :
triplets(L):={
local LR,LT,j,k,l,s;
LR:=NULL;
LT:=NULL;
s:=size(L)-1;
pour j de 0 jusque s-2 faire
pour k de j+1 jusque s-1 faire
pour l de k+1 jusque s faire
LT:=LT,[L[j],L[k],L[l]];
fpour;
fpour;
fpour;
retourne LT;
}:;
On tape pour n=12 :
LT:=triplets(idivis(12));size(LT);comb(3);comb(6,3)
On obtient :
[1,2,3],[1,2,4],[1,2,6],[1,2,12],[1,3,4],[1,3,6],[1,3,12],
[1,4,6],[1,4,12],[1,6,12],[2,3,4],[2,3,6],[2,3,12],[2,4,6],
[2,4,12],[2,6,12],[3,4,6],[3,4,12],[3,6,12],[4,6,12],20,20
On tape :
solutions(n):={
local LR,LT,L,j,k,l,s;
LR:=NULL;
LT:=NULL;
L:=idivis(n);
s:=size(L)-1;
pour j de 0 jusque s-2 faire
pour k de j+1 jusque s-1 faire
pour l de k+1 jusque s faire
LT:=LT,[L[j],L[k],L[l]];
fpour;
fpour;
fpour;
s:=size(LT)-1;
pour j de 0 jusque s faire
si irem(n,sum(LT[j]))==0 alors
LR:=LR,LT[j];
fsi;
fpour;
retourne LR;
}:;
On tape pour n=12 :
LS:=solutions(12);size(LS)
On obtient 2 solutions (sur les 20 triplets):
[1,2,3],[2,4,6],2
On tape pour n=60 :
LS:=solutions(60);size(LS)
On obtient 20 solutions (sur les 220 triplets):
[1,2,3],[1,2,12],[1,3,6],[1,4,5],[1,4,10],[1,4,15],[1,5,6],
[2,3,5],[2,3,10],[2,3,15],[2,4,6],[2,6,12],[3,4,5],[3,5,12],
[3,12,15],[4,5,6],[4,6,10],[4,6,20],[5,10,15],[10,20,30],20
On tape pour n=6279 :
LS:=solutions(6279);size(LS)
On obtient 9 solutions (sur les 560 triplets):
[1,7,13],[1,21,69],[1,69,91],[3,7,13],[3,13,23],[3,23,273],
[7,23,39],[21,91,161],[23,161,299],9
4.3 Énoncés sur l’identité de Bézout
4.3.1 L’énoncé 1
Quel est le plus petit nombre entier avec lequel il faut multiplier 49 pour
obtenir un nombre se terminant par 999999999 (9 neufs) ?
Réponse niveau primaire
On peut faire une multiplication à trous :
On trouve :
Réponse niveau collège
On a 9999999999=109−1 et le résultat de la multiplication doit être de
la forme n*109+109−1 avec 0≤ n<49 (ou de la forme p*109−1)
avec 0< p ≤ 49.
On utilise le tableur en cherchant n pour que :
n*109+109−1 soit divisible par 49.
On utilisera les commandes irem(a,b) et iquo(a,b) qui renvoient
respectivement le reste et le quotient de la division euclidienne de a
par b.
Pour cela on met dans la première colonne les nombres de 0 à 48, puis dans
la deuxième colonne les nombres n*109+109−1 pour n de 0 à 48.
Dans la troisième colonne on calcule le reste de la division de la deuxième
colonne par 49 et on trouve que pour n=33 ce reste est nul.
Il reste à calculer iquo(33*10^9+10^9-1,49) et on
trouve :
Mais cette méthode est très couteuse !
On peut aller un peu plus vite (surtout si on veut faire les calculs à la
main) en remarquant que 10=3 mod7 et que 100=2 mod49 donc :
103=−1 mod7
106=1 mod7
109=−1 mod7
108=24=16 mod49
109=13 mod49
13*−7=7 mod49
On cherche a tel que a*109=49*k+1=7*p+1.
donc −a=1 mod7 et 13*a=1 mod49
Si a=48 on a 13*a=−13=36 mod49
Si a=41 on a 13*a=13*−1+13*−7=−13+7=−6 mod49
Si a=34 on a 13*a=13*−1+13*−7+13*−7=1 mod49
Donc 34*109=1 mod49
Il reste à calculer iquo(34*10^9-1,49) et on
trouve :
Réponse niveau TS
On a : 999999999+1=109.
On cherche p pour avoir : p*49=a*109−1 c’est à dire
1=a*109−p*49.
Avec Xcas on tape :
bezout_entiers(49,10^9)
On obtient :
[306122449,-15,1]
Donc :
49*306122449−15*109=1
et puisque 49*109−49*109=0, on a :
49*(109−306122449)+(15−49)*109=−1.
Puisque 109−306122449=693877551 et (49−15)=34, on a :
| 49*693877551=34*109−1=33999999999 |
Pour faire les calculs à la main on écrit :
109=13 mod49
donc on écrit les 2 premières équations :
puisque 49=3*13+10 on soustrait 3 fois l’équation 2 à l’équation 1 et
on obtient l’équation 3 :
puisque 13=1*10+3 on soustrait l’équation 3 à l’équation 2 et
on obtient l’équation 4 :
puisque 10=3*3+1 on soustrait 3 fois l’équation 4 à l’équation 3 et
on obtient l’idendité de Bézout :
On a −15=34 mod49 et 109=13 mod49 donc
34*109−1 est divisible par 49.
Il reste à calculer iquo(34*10^9-1,49) et on
trouve :
4.3.2 L’énoncé 2
Résoudre en nombres entiers :
Avec Xcas on tape :
bezout_entiers(13,5)
On obtient :
[2,-5,1]
Donc 2*13−5*5=1.
et puisque k*13*5−k*13*5=0, on a :
13*(2+5k)−(5+13k)*5=1.
13x+5y=1 a donc comme solutions x=2+5k,y=−5−13k avec k dans ℤ.
En multipliant l’égalité 13*(2+5k)−(5+13k)*5=1 par 6 on a :
13*(12+30k)−(30+78k)*5=6
5x+13y=6 a donc comme solutions x=−30−78k,y=12+30k avec k dans ℤ.
4.4 Énoncés sur des nombres de ℤ/pℤ
4.4.1 L’énoncé 1
Trouver les 2 derniers chiffres de 1996919969.
Ici, on est sûr que le dernier chiffre est 9, puisque 19969 est un nombre
impair.
Avec Xcas, on tape :
powmod(19969,19969,100)
On obtient : 29
On peut aussi taper mais le calcul est inefficace :
irem(19969^19969,100)
4.4.2 L’énoncé 2
Trouver les 2 derniers chiffres de 1999619996.
Ici, on est sûr que le dernier chiffre est 6.
Avec Xcas, on tape :
powmod(19996,19996,100)
On obtient : 96
On peut aussi taper directement pour vérifier :
irem(19996^19996,100)
4.5 TP sur l’indicatrice d’Euler
Bijection entre ℚ ∩ [0,1] et ℕ
On construit une bijection f entre les rationnels de [0,1] et ℕ,
pour cela :
-
on ordonne les rationnels de [0,1] de la façon suivante :
- on supprime les fractions non irréductibles et on obtient une suite
L.
La fonction f attribue à un rationnel de [0,1] son rang dans la
suite L, on a :
f(0)=0, f(1)=1, f(1/2)=f(2/4)=2, f(1/3)=3...,
f(3/4)=6,..., f(1/5)=7....
-
Déterminer le nombre d’éléments de L qui a comme dénominateur
23 (resp 24, 25...30), à l’aide de l’indicatrice d’Euler,
- Déterminer f(1/7) puis f(1/30), f(13/30)
et f(29/30),
- Écrire un programme qui etant donné deux entiers a et b (a<b)
renvoie la liste des entiers plus petit que a qui sont premiers avec b,
- Écrire un programme qui définit la fonction f ayant pour variable
une fraction r de [0,1],
- Écrire un programme qui pour n>0 trace les points
de coordonnées a/b,f(a/b) avec b ≤ n. Afficher
les points de coordonnées a/b,f(a/b) avec b<=32
- Amusez vous à tracer ces points avec une couleur qui varie selon la
valeur a de a/b.....
4.5.2 Le corrigé avec Xcas
On utilise la fonction euler de Xcas qui est l’indicatrice d’Euler
c’est à dire euler(n) renvoie le nombre d’entiers inférieurs à
n qui sont premiers avec n
(euler(n)=card({p<n,gcd(n,p)=1})).
-
Le nombre d’éléments de L qui a comme dénominateur 23 est
le nombre d’entiers inférieur à 23 qui sont premiers avec 23 c’est donc
euler(23).
On tape :
euler([23,24,25,26,27,28,29,30])
On obtient :
[22,8,20,12,18,12,28,8]
On a :
f(1/5) est euler(1)+euler(2)+...+euler(4)+1
On vérifie, on sait que f(1/5)=7 et
sum(euler(n),n,1,4)+1 vaut bien 7.
On a :
f(1/7) est euler(1)+euler(2)+...+euler(6)+1 donc on tape :
sum(euler(n),n,1,6)+1
On obtient f(1/7) :
13
On tape :
sum(euler(n),n,1,29)+1
On obtient f(1/30):
271
Pour avoir f(13/30), il faut
avoir le cardinal des entiers p>1 qui sont premiers avec 30 et inférieurs
ou égaux à 13. Les nombres premiers inférieurs ou
égaux à 13 sont 2,3,5,7,11,13 et ifactor(30)=2*3*5
Donc f(13/30)=f(1/30)+3=274.
Puisque 29/30 est le plus grand élément de dénominateur 30,
pour avoir f(29/30), on tape :
sum(euler(n),n,1,30)
On obtient la valeur de f(29/30) :
278
On sait que euler(30)=8 et les 8 entiers inférieurs ou
égaux à 30 qui sont premiers avec 30 sont :
1,7,11,13,17,19,23,29.
- On peut aussi
écrire un petit programme qui renvoie la liste des entiers
plus petit que a et premier avec b :
Lppapremb(a,b):={
local L,k;
L:=NULL;
for (k:=1;k<=a;k:=k+1){
if (gcd(k,b)==1) {
L:=L,k;
}
}
return [L];
}:;
On tape :
sum(euler(n),n,1,29)+size(Lppapremb(1,30))
On obtient f(1/30) :
271
On tape :
sum(euler(n),n,1,29)+size(Lppapremb(13,30))
On obtient f(13/30) :
274
On tape :
sum(euler(n),n,1,29)+size(Lppapremb(29,30))
On obtient f(29/30):
278
- Pour avoir la valeur de f(a/b) il suffit connaitre la longueur s de la
liste des entiers plus petit que a et premier avec b .
On utilise les fonction numer (resp denom)
qui renvoie le numerateur (resp dénominateur) de la fracton simplifiée.
On tape :
f(r):={
local s,k,a,b;
a:=numer(r);
b:=denom(r);
s:=0;
for (k:=1;k<=a;k:=k+1){
if (gcd(k,b)==1) {s:=s+1;}
}
return sum(euler(n),n,1,b-1)+s;
}:;
On tape :
f(1,30)
On obtient f(1/30) :
271
On vérifie en tapant :
1+sum(euler(k),k=0..29) et on obtient bien 271
On tape :
f(13,30)
On obtient f(13/30) :
274
On tape :
f(29,30)
On obtient f(29/30) :
278
On vérifie en tapant :
sum(euler(k),k=0..30) et on obtient bien 278
On tape :
f(31,32)
On obtient f(31/32):
324
On tape :
f(39,40)
On obtient :
490
- Pour tracer les points
de coordonnées a/b,f(a/b),
on ne se sert pas de la fonction f mais on calcule sa valeur au fur et à
mesure et on la met dans la variable valf : à chaque étape
valf augmente de 1.
tracef(n):={
local L,a,b,valf;
L:=point(0),point(1);
valf:=1;
for (b:=2;b<=n;b:=b+1){
for (a:=1;a<b;a:=a+1){
if (gcd(a,b)==1) {
valf:=valf+1;
L:=L,point(evalf(a/b)+i*valf);
}
}
}
return affichage(L,rouge+point_point+
epaisseur_point_2);
}:;
On tape :
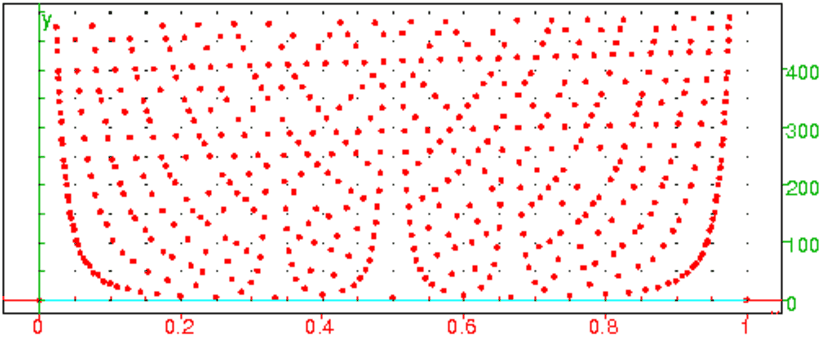
tracef(40)
On obtient :
Remarque
Si on tape
tracer(n):={
local L,a,b;
L:=point(0),point(1);
for (b:=2;b<n;b:=b+1){
for (a:=1;a<b;a:=a+1){
if (gcd(a,b)==1){L:=L,point(evalf(a/b)+i*f(a/b));}
}
}
return affichage(L,rouge+point_point+
epaisseur_point_2);
}:;
Le temps de réponse est beaucoup plus long car le programme calcule à
chaque ètape f(a/b) sans tenir compte des valeurs de f
calculées auparavant. Le temps mis pour faire
tracer(100) est de 160.02s alors que celui de
tracef(100) est de 3.52s.
On peut encore diminuer le temps de calcul en stockant par référence
(avec =< au lieu de :=) les
points dans la liste L. Pour cela il faut connaitre la longueur s
de la liste L qui est f((n-1)/n).
On tape :
tracerf(n):={
local L,a,b,valf,s,j;
s:=f((n-1)/n);
L:=makelist(0,1,s);
L[0]=<point(0);
L[1]=<point(1);
valf:=1;
j:=2;
for (b:=2;b<=n;b:=b+1){
for (a:=1;a<b;a:=a+1){
if (gcd(a,b)==1) {
valf:=valf+1;
L[j]=<point(evalf(a/b)+i*valf);
j:=j+1;
}
}
}
return affichage(L,rouge+point_point+
epaisseur_point_2);
}:;
On tape :
tracerf(100)
On obtient en 0.89s :
- On met un peu de couleur ....
On tape :
tracerfc(n):={
local L,a,b,valf,s,j;
s:=f((n-1)/n);
L:=makelist(0,1,s);
L[0]=<point(0);
L[1]=<point(1);L:=point(0),point(1);
valf:=1;j:=2
for (b:=2;b<=n;b:=b+1){
for (a:=1;a<b;a:=a+1){
if (gcd(a,b)==1) {
valf:=valf+1;
L[j]=<point(evalf(a/b)+i*valf,affichage=
irem(a,7)+point_point+epaisseur_point_2);
j:=j+1;
}
}
}
return L;
}:;
On tape :
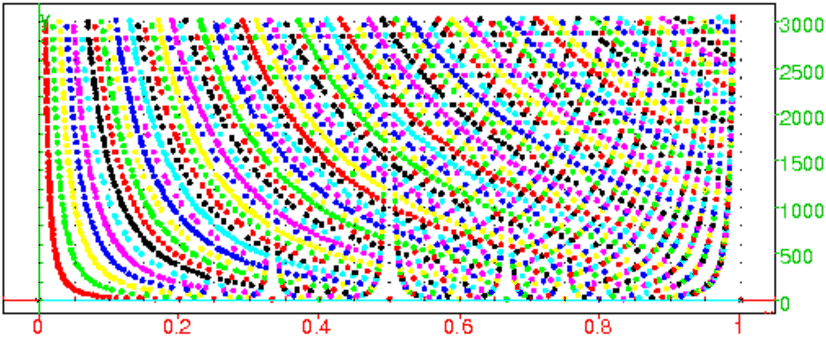
tracerfc(100)
On obtient en 0.84s :
On remarque que les points (1/(n+1),f(1/(n+1))) et les points
((n−1)/n,f((n−1)/n)) semblent être sur des courbes symétriques par rapport
à x=1/2, cela s’explique puisque f((n−1)/n)+1=f(1/(n+1)).
4.5.3 Prolongement du TP sur l’indicatrice d’Euler
Approximation d’un nuage de points
La fonction f est la bijection entre ℚ ∩ [0,1] et ℕ qui a èté
définie dans le TP précédent.
-
À l’aide du tableur tracer le nuage de points de coordonnèes :
1/n,f(1/n) où f est la fonction définie
précédement. On rappelle que l’on a :
où Φ est la fonction d’Euler.
- On se demande si ces points sont sur une courbe identifiable. Dans le
livre d’Hardy and Wright d’introduction à la théorie des nombres, il est
dit que ∑k=0n−1Φ(k)≃ 3n2/π2 pour
n grand. Vérifier ce résultat en utilisant une régression convenable.
- Faites une simulation pour vérifier que si on tire au hasard deux
entiers et qu’avec ces 2 entiers on forme une fraction de ]0;1], la
probabilité d’obtenir une fraction irréductible est égale à 6/π2.
- Faites une simulation pour vérifier que si on tire au hasard deux
entiers la probabilité d’obtenir deux entiers premiers entre eux est égale
à 6/π2.
4.5.4 Corrigé du prolongement du TP sur l’indicatrice d’Euler
-
On ouvre le tableur avec par exemple 100 lignes.
-
dans la colonne A, on met la suite des nombres
entiers 1,2....,
- dans la colonne B, on met l’inverse de ces nombres.
Pour cela on met dans B0 : 1 et dans B1 : =$B$0/A1 ou
plus simplement =1/A1.
Puis on copie cette formule vers le bas.
- dans la colonne C, on met dans C0 : 1,
dans C1 : =euler(A0)+C0 et dans C2 : =euler(A1)+C1.
Puis on copie cette formule vers le bas.
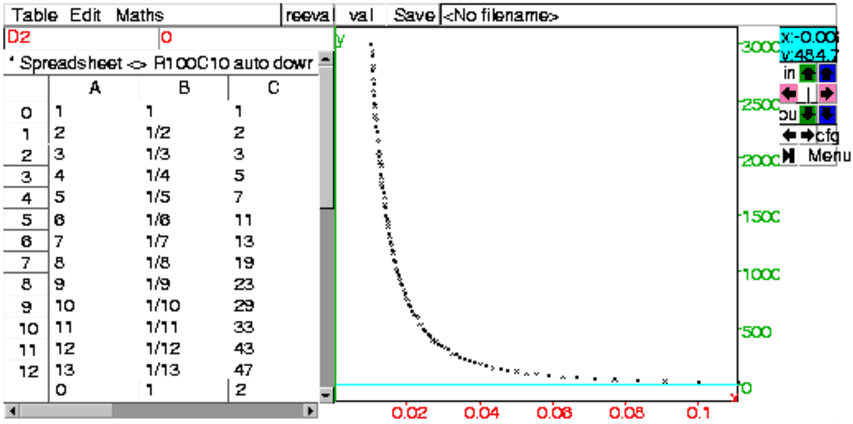
On sélectionne les 2 colonnes B et C, puis dans le menu
Maths->2-d stats on choisit nuage de points la plage de cellule est alors : B0:C99 et la cellule cible D0 si on a coché
Graphe et décoché Paysage dans la configuration du tableur.
On obtient :
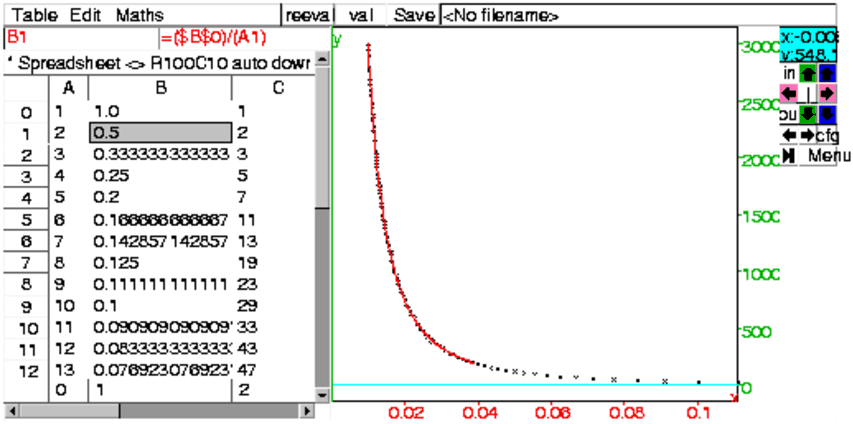
- On modifie B0 en 1.0 pour avoir des nombres approchés dans
la colonne B. Puis on sélectionne les 2 colonnes B et C,
puis dans le menu Maths->Regressions on choisit Puissance la plage
de cellule est alors : B40:C99 et la cellule cible D1 (on a coché
Graphe et décoché Paysage dans la configuration du tableur),
puis on modifie D1 en :
=power_regression_plot(matrix(50,2,(B50):(C99)),color=rouge) et on
obtient en rouge :
- on met dans D2 =(M:=matrix(60,2,(B40):(C99))).
Puis on tape :
=power_regression(M)
On obtient :
-2.01348683765,0.283029041082
Ce qui veut dire que y=0.283029041082*x−2.01348683765 approche la courbe
y=f(x), c’est à dire que f(1/n)≃ 0.283029041082*n2.01348683765.
On tape : evalf(3/pi^2)
On obtient : 0.303963550927
- On écrit tout d’abord le programme :
fractirred0(n,p):={
local a,b,j,k;
randseed;
k:=0;
pour j de 1 jusque p faire
a:=rand(n)+1;
b:=rand(n)+1;
si gcd(a,b)==1 alors k:=k+1;fsi;
fpour;
retourne evalf(k/p),evalf(6/pi^2);
}:;
On tape :
fractirred0(100000,1000000)
On obtient :
0.607658,0.607927101854
On tape :
fractirred0(1000000,1000000)
On obtient :
0.607544,0.607927101854
On tape :
fractirred0(2^31,10^6)
On obtient :
0.607876,0.607927101854
Mais ce programme n’est pas correct car pour le couple (a,b) peut prendre
n2 valeurs alors que les fractions a/b ∈ ]0;1] avec b≤ n sont au
nombre de n(n+1)/2.
fractirred1(n,p):={
local a,b,j,k;
randseed;
k:=0;
pour j de 1 jusque p faire
b:=rand(n)+1;
repeter a:=rand(n)+1;jusqua a<=b;
si gcd(a,b)==1 alors k:=k+1;fsi;
fpour;
retourne evalf(k/p),evalf(6/pi^2);
}:;
On tape :
fractirred1(10000,10000)
On obtient :
0.6065,0.607927101854
Mais l’exécution rique d’être longue car si on a tirer pour b 0 ou 1,
trouver un a plus petit risque de prendre du temps !!!!
Pour faire un programme plus "rigoureux", on va numéroter les fractions sans
enlever les fractions réductibles (par ex le rang de 2/2 est 3 et celui de 2/6
est 17) puis tirer au hasard un nombre dans
(1,2,...n(n+1)/2) et chercher la fraction ayant ce rang comme valeur.
On tape :
randfract(n):= {
local r,a,p,q;
a:=n*(n+1)/2;
r:=rand(a)+1;
q:=floor((-1+sqrt(8*r+1))/2);
p:=r-q*(q+1)/2;
retourne p,q;
}:;
fractirred(n,p):={
local a,b,j,k;
randseed;
k:=0;
pour j de 1 jusque p faire
a,b:=randfract(n);
si gcd(a,b)==1 alors k:=k+1;fsi;
fpour;
retourne evalf(k/p),evalf(6/pi^2);
}:;
On tape :
fractirred(1000,10000)
On obtient :
0.6059,0.607927101854
On tape :
fractirred(60000,100000)
On obtient :
0.60509,0.607927101854
Remarque
Calculons la probabilité d’avoir une fraction irréductible parmi toutes
les fractions de ]0;1] qui ont un dénominateur d≤ n.
Le nombre total de ces fractions est n(n+1)/2, en effet il y a :
1 fraction de dénominateur 1,
2 fractions de dénominateur 2,..
n fractions de dénominateur n
donc en tout n(n+1)/2 fractions de ]0;1] de dénominateur d≤ n,
Le nombre des fractions irréductibles parmi ces fractions est
∑k=1neuler(k), en effet il y a :
euler(1)=1 fraction irréductible de dénominateur 1,
euler(2)=1 fraction irréductible de dénominateur 2,..
euler(n) fractions irréductibles de dénominateur n
donc en tout euler(1)+euler(2)+..+euler(n) fractions irréductibles de
dénominateur d≤ n.
On tape :
2*sum(euler(k),k=1..1000)/(1000^2+1000.)
On obtient :
0.607776223776
On tape :
2*sum(euler(k),k=1..10000)/(10000^2+10000.)
On obtient :
0.607888931107
Si on suppose que n est grand et que l’on a montré que
∑k=0n−1Φ(k)≃ 3n2/π2, la probabilité d’avoir une
fraction irréductible parmi toutes
les fractions de [0;1] qui ont un dénominateur d≤ n est :
∑k=1n euler(k)≃ 2*3*(n+1)2/π2*n*(n+1)=6*(n+1)/nπ2.
Cette probabilité tend donc vers 6/π2 quand n tend vers
l’infini.
Idée pour montrer que si on tire au hasard 2 nombres entiers, la
probabilité d’obtenir deux entiers premiers entre eux est égale à
6/π2
Cette propriété résulte du fait que π2/6 est la somme de la
série de terme général un=1/n2 i.e.
∑n=1+∞1/n2=π2/6.
En effet, soit p un nombre premier.
La probabilité pour qu’un entier pris au hasard soit divisible par p (i.e.
multiple de p) est égale à 1/p (la probabilité
pour qu’un entier pris au hasard soit divisible pair est égale à
1/2, la probabilité pour qu’un entier pris au hasard soit
divisible par 3 est égale à 1/3...)
La probabilité pour que deux entiers pris au hasard soient tous les deux
divisibles par p est égale à 1/p2.
Donc la probabilité pour que le pgcd de deux entiers pris au
hasard ne soit pas divisible par p est égale à 1−1/p2.
Donc, si NP est l’ensemble des nombres premiers, la probabilité pour que le
pgcd de deux entiers pris au hasard soit égal à 1 (i.e. divisible par aucun
nombre premier) est égale à Πp∈ NP(1−1/p2).
Il faut maintenant écrire autrement Πp∈ NP(1−1/p2) ou
plutôt son inverse Πp∈ NP1/1−1/p2.
On sait que 1/1−t2=∑n=0+∞t2n donc
1/1−1/p2=∑n=0+∞1/p2n.
Finallement Πp∈ NP1/1−1/p2=Πp∈ NP∑n=0+∞1/p2n
Comme les nombres entiers sont le produit de nombres premiers une certaine
puissance, on a :
Πp∈ NP1/1−1/p2=Πp∈ NP∑n=0+∞1/p2n =∑k=0+∞1/k2=π2/6.
Ainsi Πp∈ NP(1−1/p2)=6/π2
4.6 Le problème de Joseph Bertrand (1822-1900)
Soit un cercle de rayon R. On appelle corde type les cordes de longueur
a=R√3. La longueur des cordes types est égale à la longueur des
côtés des triangles équilatéraux inscrits dans ce cercle. Le problème
de Joseph Bertrand est :
quelle est la probabilité pour qu’une corde prise au hasard soit plus grande
qu’une corde type ?
Écrire un programme qui simule le choix d’une corde prise au hasard dans un
cercle de rayon 1 lorsque :
-
On prend 2 points au hasard sur le cercle pour déterminer une corde,
- On prend 1 point au hasard sur le cercle et une direction au hasard ce
qui déterminera une corde.
- On prend 1 point défini au hasard par ses coordonnées cartésiennes
dans le cercle. Ce point déterminera le milieu de
la corde (et donc la corde),
- On compare les cordes qui ont la même direction : pour cela, pour
chaque direction d, on prend un réel r au hasard entre
−R et R et cela défini 1 point sur le rayon orthogonal à d. Ce point
déterminera le milieu de la corde (et donc la corde).
Puis expliquez les résultats obtenus.
Les programmes avec Xcas
Une corde type AB d’un cercle de rayon 1 a pour longueur √3 et son
angle au centre vaut 2π/3 i.e si a est l’argument de l’affixe de A et
b est l’argument de l’affixe de B.
-
On prend 2 points A et B au hasard sur le cercle pour déterminer
une corde. Ces 2 points seront déterminés par leur arguments a et b
choisis au hasard entre −π0 et π. Ces deux points définissent une
corde de longueur supérieure à √3 si
l=AB2=abs(exp(i*a)−exp(i*b))2=2−2cos(a−b)> 3 ou si
2π/3<|a−b|<4π/3.
Cela donne les 2 programmes simulber10 et simulber11.
Le programme simulber10 étant plus rapide puisqu’il nécessite qu’un
seul test.
On tape :
simulber10(n):={
local j,a,b,l,s;
s:=0;
pour j de 1 jusque n faire
a:=rand(-pi,pi);
b:=rand(-pi,pi);
l:=2-2*cos(a-b);
si l>3 alors s:=s+1; fsi;
fpour;
retourne s,n,evalf(s/n);
}:;
simulber11(n):={
local j,a,b,c,s;
s:=0;
pour j de 1 jusque n faire
a:=rand(-pi,pi);
b:=rand(-pi,pi);
c:=abs(a-b);
si c>2*pi/3 et c<4*pi/3 alors s:=s+1; fsi;
fpour;
retourne s,n,evalf(s/n);
}:;
On tape :
simulber10(100000)
On obtient : 33315,100000,0.33315
On tape :
simulber11(100000)
On obtient : 33410,100000,0.3341
Dans ces 2 programmes ce qui compte c’est la valeur de |b−a| qui est un
nombre entre 0 et 2π. Il y a donc une chance sur trois pour que ce nombre
soit compris entre 2π/3 et 4π/3.
- On prend 1 point A au hasard sur le cercle et une direction d au
hasard pour déterminer une corde. Le point A sera déterminé par son
argument a choisi au hasard entre −π et π et la direction D par son
angle d avec l’axe des x que l’on choisit au hasard entre 0 et π.
Ce point et la direction définissent une corde AB de longueur supérieure
à √3 si (a+b)/2=π/2−d (c’est à dire b=π+2d−a).
On tape :
simulber2(n):={
local j,a,b,d,l,s;
s:=0;
pour j de 1 jusque n faire
a:=rand(-pi,pi);
d:=rand(0,pi);
b:=pi+2*d-a;
l:=2-2*cos(a-b);
si l>3 alors s:=s+1; fsi
fpour
retourne s,n,evalf(s/n);
}:;
On tape :
simulber2(100000)
On obtient : 33264,100000,0.33264
On a le même résultat qu’en 1, puisque c’est pratiquement le même
programme.
- On définit au hasard dans le cercle le milieu de la corde par ses
coordonnées cartésiennes.
simulber3(n):={
local j,a,b,c,l,s;
s:=0;
pour j de 1 jusque n faire
repeter
a:=rand(-1,1);
b:=rand(-1,1);
jusqua a^2+b^2<1;
l:=4*(1-a^2-b^2);
si l>3 alors s:=s+1; fsi;
fpour;
retourne s,n,evalf(s/n);
}:;
On peut remplacer
l:=4*(1-a^2-b^2);si l>3 alors s:=s+1; fsi; par
l:=a^2+b^2;si l<1/4 alors s:=s+1; fsi;
On tape :
simulber3(100000)
On obtient : 25039,100000,0.25039
Le cercle de rayon 1/2 a comme surface π/4 et celui de rayon 1 a comme
surface π. La probabilité de se trouver dans le cercle de rayon 1/2 est
donc de 1/4.
Attention Si on écrit :
simulber30(n):={
local j,a,b,c,l,s;
s:=0;
pour j de 1 jusque n faire
a:=alea(-1,1);
c:=sqrt(1-a^2);
b:=alea(-c,c);
l:=4*(1-a^2-b^2);
si l>3 alors s:=s+1; fsi;
fpour;
retourne s,n,evalf(s/n);
}:;
le programme n’est pas correct car dans ce programme a et b ne sont pas
indépendants (voir la remarque du 13.13).
On tape :
simulber30(100000)
On obtient : 20311,100000,0.20311
On fait le calcul de la probabilité avec ce programme.
La probabilité d’avoir : a<x<a+da et b<y<db est :
da*db/aire(S) avec S={(x,y) a<x<a+da,0<y<√1−a2}.
On obtient si cos(t1)=a et cos(t2)=a+da: avec dt=−da/√1−a2
aire(S)=2(t1−t2)+sin(2t2)−sin(2t1)=2dt(cos(2t1)−1)=4da√1−a2
donc db=1/(4√1−a2)
On a :
∫01√(1−x2)/√(1−x2)dx=1 donc la probbilité d’être
dans le cercle de rayon 1/2 est :
∫01/2√(1/4−x2)/√(1−x2)dx
0n tape
romberg(sqrt((1/4-x^2))/sqrt((1-x^2)),x=0..1/2)
On obtient (avec 7 digits) : 0.20315486 - On définit au hasard un nombre réel r entre −R et R. la longueur
l de la corde de direction d et dont la distance au centre est
r est : l=2√1−r2 et l ne dépend pas de la direction. Donc pour
une direction donnée la probabilité cherchée ne dépend pas de la
direction.
On tape (dans le programme R=1 etl est le carré de la longueur de la corde) :
simulber4(n):={
local j,r,l,s;
s:=0;
pour j de 1 jusque n faire
r:=rand(-1,1);
l:=4*(1-r^2);
si l>3 alors s:=s+1; fsi
fpour
retourne s,n,evalf(s/n);
}:;
On tape :
simulber4(100000)
On obtient : 49993,100000,0.49993
En effet, on a l=AB2=4*(1−r2) et donc les conditions l>3 et 0<r<1/2
sont équivalentes.
Donc pour une direction donnée la probabilité cherchée est 1/2 et elle
ne dépend pas de la direction.œn en conclut que par rapport à la corde type,
il y a autant de cordes longues que de cordes courtes.
Remarque
Lorsqu’on définit au hasard dans le cercle le milieu M de la corde par ses
coordonnées polaires r,t (i.e. l’affixe de M est m=rexp(it)).
Pour cela on choisit un réel r au hasard entre
−R et R et un angle t réel au hasard entre 0 et π ce qui
déterminera le point r exp(it).
On tape :
simulber40(n):={
local j,r,t,m,l,s;
s:=0;
pour j de 1 jusque n faire
r:=rand(-1,1);
t:=rand(0,pi);
m:=r*exp(i*t);
l:=4*(1-r^2);
si l>3 alors s:=s+1; fsi
fpour
retourne s,n,evalf(s/n);
}:;
On tape :
simulber40(100000)
On obtient : 50068,100000,0.50068
En effet, on voit que la valeur de t ne sert pas et que l=AB2 ne
dépend que de r. Les conditions l>3 et 0<r<1/2 sont équivalentes.
Donc la probabilité cherchée est encre 1/2.
Question Pourquoi selon que l’on choisit le milieu de la corde avec ses
coordonnées cartésiennes ou avec ses coordonnées polaire la probabilité
passe de 1/4 à 1/2 ?
Il faut comprendre que :
r:=rand(-1,1);
t:=rand(0,pi);
M:=point(r*exp(i*t));
ne définit pas des points équirépartis dans le cercle de centre 0 et de
rayon 1.
Il y a plus de points proche du centre que sur la périphérie (voir la remarque du 13.13).
4.7 Un exercice sur les congruences et les restes chinois
Trouver un nombre entier n vérifiant 4<n<N vérifiant :
n est divisible par 2
n−1 est divisible par 3
n−2 est divisible par 5
n−3 est divisible par 7
n−4 est divisible par 11
4.7.2 Solution avec Xcas et les restes chinois
On utilise la commande ichinrem.
On tape :
ichinrem([0%2,1%3,2%5,3%7,4%11]))
On obtient :
-788 % 2310
On veut que 0<n<N donc :
n=(2310−788)+2310*k=1522+2310*k avec k≤ iquo((N−1522),2310)
donc si N=10000 on tape :
iquo((10000-1522),2310)
On obtient :
3
On tape :
(1522+2310*k)$(k=0..3)
On obtient :
1522,3832,6142,8452
4.7.3 Solution avec Xcas et l’identité de Bézout
On utilise la commande iabcuv qui étant donné trois entiers
a,b,c renvoie une liste de deux entiers
relatifs [u,v] vérifiant a*u+b*v=c.
Remarque
-
Si deux entiers
relatifs u,v vérifie au+bv=c alors on a aussi :
a(u+kb)+b(v−ka)=c pour tout k ∈ ℤ.
- iabcuv est une généralisation de l’identité de Bézout
(commande iegcd). On a en effet :
iegcd(a,b) renvoie une liste de trois entiers [u,v,d]
vérifiant a*u+b*v=d=gcd(a,b) (où gcd(a,b) est
le pgcd de a et b).
Donc pour que iabcuv ait une solution il faut et il
suffit que c soit un multiple du pgcd de a et b.
Donc iabcuv a toujours une solution si a et b sont premiers
entre eux.
On cherche n vérifiant :
n est un multiple de 2 et aussi un multiple de 3 plus 1.
Donc on a : n=2p=3q+1 avec p∈ ℤ et q∈ ℤ.
c’est à dire 2p−3q=1.
On tape : iabcuv(2,3,1)
On obtient : [-1,1]
Donc n=2*(−1+3k)=−2 % 6.
De plus n est un multiple de 5 plus 2.
Donc on a : n=5r+2=−2+6k avec r∈ ℤ et k∈ ℤ.
c’est à dire 6k−5r=4.
On tape : iabcuv(6,5,4)
On obtient : [-1,2]
Donc n=6*(−1+5k)−2=−8 % 30.
De plus n est un multiple de 7 plus 3.
Donc on a : n=7j+3=−8+30k avec j∈ ℤ et k∈ ℤ.
c’est à dire 30k−7j=11.
On tape : iabcuv(30,7,11)
On obtient : [2,-7]
Donc n=30*(2+7k)−8=52 % 210.
De plus n est un multiple de 11 plus 4.
Donc on a : n=11m+4=52+210k avec m∈ ℤ et k∈ ℤ.
c’est à dire 11m−210k=48.
On tape : iabcuv(11,210,64)
On obtient : [-72,4]
Donc n=11*(−72+210k)+4=−788 % 2310.
On tape : (-788+k*2310)$ (k=1..4)
On obtient : 1522,3832,6142,8452
Retour à la page personnelle de Bernard Parisse.