We have :
0.1 = 2-4*(1 + 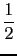 +
+ 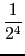 +
+ 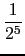 +
+ 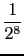 +
+ 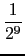 + ...) = 2-4*
+ ...) = 2-4*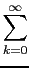 (
(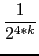 +
+ 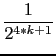 )
)
hence 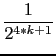 )
)
3f (00111111), b9 (10111001), 99 (10011001), 99 (10011001), 99 (10011001), 99 (10011001), 99 (10011001), 9a (10011010),the last octet is 1010, indeed the 2 last bits 01 became 10 because the following digit is 1 (upper rounding).
Computing a is done by adjusting exponents (here nothing to do), then substract the mantissa, and adjust the exponent of the result to have a normalized float. The exponent is
3f (00111111), b9 (10111001), 99 (10011001), 99 (10011001), 99 (10011001), 99 (10011001), 99 (10011001), 9a (10100000),Therefore a > 0.1 and a - 0.1 = 1/250 +1/251 (since 100000-11010=110)