où 
et 
sont les symboles
principaux de deux solutions BKW issues respectivement de
et 
(on rappelle que 
est le vecteur tangeant en un point de la géodésique d'Agmon
reliant à exprimé dans la
base de matrices 
).
La preuve de ce résultat est purement calculatoire. La première égalité se prouve comme dans [4, équations (63), (64),]. On a:
car
. De plus
, donc:
D'où:
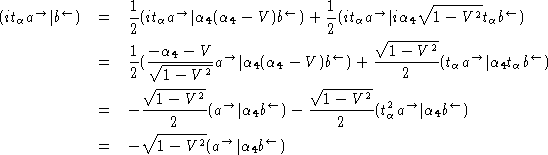
Passons à la deuxième égalité de (31). Comme
est normé et orthogonal à 
, on a:
Donc, en posant 
:
On décompose maintenant les symboles BKW en leur partie norme et leur partie de type y. Il s'agit donc d'estimer des produits scalaires du type:
où 
et 
sont solutions
déquations de transport du type (13). Il faut remarquer que
les abscisses curvilignes définies par (13) croissent en
sens opposés pour et . Si on
choisit le sens croissant pour , alors:
Donc:
car 
anticommute avec les 
(on
utilise aussi le fait que les sont hermitiennes). Il
suffit donc d'estimer le produit scalaire en . En
ce point, la situation est simple car vaut 
sur
Ker 
et:
Finalement, il suffit de connaitre les solutions au puits dont elles sont issues.
Dans le calcul de la matrice d'interaction, 
prendra deux valeurs: 
et 
qui
forment une base de Ker 
.
Preuve
Soit 
un vecteur propre normé de 
associé à 
. Il existe alors 
et 
tels
que:
Comme K est antilinéaire de carré -Id, on a alors:
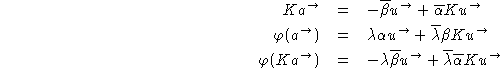
Donc, comme 
est
orthonormée:
et:
On conclut alors aisément.
