Chapitre 15 Les carrés magiques

15.1 Les matrices magiques d’odre 3

15.1.1 Résultat préliminaire

Soit A la matrice :
A=[[a₀₀,a₀₁,a₀₂],[a₁₀,a₁₁,a₁₂],[a₂₀,a₂₁,a₂₂]] Montrer que :
B=1/2*(A+tran(A)) est une matrice symértrique et
C=1/2*(A−tran(A)) est une matrice antisymértrique.
En déduire que toute matrice se décompose de façon unique en la somme d’une matrice symétrique et d’une matrice antisymétrique.
On tape :
A:=[[a00,a01,a02],[a10,a11,a12],[a20,a21,a22]]
B:=1/2*(A+tran(A));C:=1/2*(A-tran(A))
normal(B-tran(B)),normal(C+tran(C))
On obtient :
[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]]
Si A=M+N avec tran(M)=M et tran(N)=−N alors tran(A)=M−N donc
M=1/2*(A+tran(A))=B et N=1/2*(A−tran(A))=C d’où l’unicité.

15.1.2 Les matrices magiques d’ordre 3

Une matrice A=(a_j,k) d’ordre 3 est une matrice magique de somme s lorsque les 8 sommes :
∑_j=0²a_j,k=s pour k=0,1,2 (somme de chaque colonne)
∑_k=0²a_j,k=s pour j=0,1,2 (somme de chaque ligne)
∑_j=0²a_j,j=a_1,3+a_2,2+a_3,1=s (somme de chaque diagonale).
Déterminer les matrices magiques d’ordre 3 qui sont antisymétriques.
Déterminer les matrices magiques d’ordre 3 qui sont symétriques de somme s=0.
Déterminer une matrice magique d’ordre 3, symétrique, de somme s et la plus simple possible.
Montrer que la différence de 2 matrices symétriques magiques de somme s est une matrices symétriques magiques de somme s=0.
En déduire toutes les matrices magiques d’ordre 3, symétriques de somme s.
Trouver toutes les matrices magiques d’ordre 3 de somme s=3.
Trouver toutes les matrices magiques d’ordre 3 de somme s=9.
Les matrices magiques d’ordre 3 qui sont antisymétriques sont de somme s=0 car la diagonale principale ne contient que des 0.
Soit A une matrice antisymétrique d’ordre 3 et magique de somme s=0.
On tape :
A:=[[0,a,b],[-a,0,c],[-b,-c,0]]
linsolve([a+b=0,-a+c=0,b+c=0],[a,b,c])
On obtient :
[c,-c,c]
Donc les matrices magiques A d’ordre 3 qui sont antisymétriques sont :
A=(

0	c	−c
−c	0	c
c	−c	0

)=c(

0	1	−1
−1	0	1
1	−1	0

)
On tape :
A:=c*[[0,1,-1],[-1,0,1],[1,-1,0]]
Soit S une matrice symétrique d’ordre 3 et magique de somme s=0.
On tape :
S:=[[a,b,c],[b,d,e],[c,e,f]]
linsolve([a+b+c,a+d+f,b+d+e,c+e+f,2c+d],[a,b,c,d,e,f])
On obtient :
[-f,f,0,0,-f,f]
Donc les matrices magiques S d’ordre 3 qui sont symétriques de somme s=0 sont :
S=(

−f	f	0
f	0	−f
0	−f	f

)=f(

−1	1	0
1	0	−1
0	−1	1

)
Soit S₀ une matrice symétrique d’ordre 3 et magique de somme s la plus simple possible.
On tape :
S0:=s/3*[[1,1,1],[1,1,1],[1,1,1]]
Donc les matrices magiques S d’ordre 3 qui sont symétriques de somme s sont B:=S+S₀:
On tape :
f*[[-1,1,0],[1,0,-1],[0,-1,1]]+s/3*[[1,1,1],[1,1,1],[1,1,1]]

Donc les matrices magiques M d’ordre 3 qui sont de somme s=3 (resp s=12) sont M:=A+S+S₀ et elles dépendent de 2 paramètres c et f.
On tape :
M:=c*[[0,1,-1],[-1,0,1],[1,-1,0]]+ f*[[-1,1,0],[1,0,-1],[0,-1,1]]+[[1,1,1],[1,1,1],[1,1,1]]
On obtient :
[[-f+1,c+f+1,-c+1],[-c+f+1,1,c-f+1],[c+1,-c-f+1,f+1]]
Par exemple f=1,c=0, on obtient [[0,2,1],[2,1,0],[1,0,2]].
On tape :
M:=c*[[0,1,-1],[-1,0,1],[1,-1,0]]+ f*[[-1,1,0],[1,0,-1],[0,-1,1]]+4*[[1,1,1],[1,1,1],[1,1,1]]
On obtient :
[[-f+4,c+f+4,-c+4],[-c+f+4,4,c-f+4],[c+4,-c-f+4,f+4]]
Par exemple f=1,c=3, on obtient un carré magique eulérien (les entiers 0..8 apparaissent dans les 9 cases du carré) : [[3,8,1],[2,4,6],[7,0,5]].

15.2 Les carrés magiques eulériens et latins pandiagonaux

Ce qui suit a èté inspiré par une épreuve à l’oral de l’agrégation externe de Mathématiques session 2005 dont voila le lien :
http://agreg.dnsalias.org/Textes/561.pdf
et par le livre Problèmes plaisants et délectables par Claude-Gaspar Bachet sieur de Mérignac.

15.2.1 Définitions

carré magique d’ordre n veut dire que l’on a une matrice carrèe de dimension n, à coefficients dans ℕ et telle que les sommes des éléments de chaque ligne, de chaque colonne et de chacune des 2 diagonales sont égales :
si A=a_j,k pour j=0..n−1,k=0..n−1 on a :
∑_k=0ⁿ⁻¹a_j,k=s pour j=0..n−1
∑_j=0ⁿ⁻¹a_j,k=s pour k=0..n−1
∑_j=0ⁿ⁻¹a_j,j=s
∑_j=0ⁿ⁻¹a_j,n−j−1=s
carré latin d’ordre n veut dire que les entiers 0..n−1 apparaissent dans chaque ligne, dans chaque colonne et dans les 2 diagonales du carré. La somme s est alors égale à n(n−1)/2
carré latin pandiagonal d’ordre n veut dire que l’on a un carré magique latin qui possède en plus la propriété : les entiers 0..n−1 apparaissent aussi dans les n diagonales brisées du carré (lorsqu’on considère le carré comme un tore). La somme s est égale à n(n−1)/2
carré eulérien d’ordre n veut dire que chacun des entiers 0..n²−1 apparaissent dans les n² cases du carré. La somme s est alors égale à n(n²−1)/2
carré eulérien pandiagonal d’ordre n veut dire que l’on a un carré magique eulérien d’odre n qui possède en plus la propriété : la somme de chacune des 2n−2 diagonales brisées (lorsqu’on considère le carré comme un tore) vaut aussi n(n²−1)/2.

15.2.2 Les carrés magiques latins pandiagonaux

Écrire un programme Xcas qui teste si une matrice est un carré magique latin pandiagonal.
On tape dans un éditeur de programme :

estlatinp(A):={
local s,n,j,k,L;
n:=size(A);
pour j de 0 jusque n-1 faire
L:=A[j];
si is_permu(L)==0 alors retourne faux; fsi;
fpour;
pour j de 0 jusque n-1 faire
L:=col(A,j);
si is_permu(L)==0 alors retourne faux; fsi;
fpour;
pour j de 0 jusque n-1 faire
L:=A[k,irem(j+k,n)]$(k=0..n-1);
si is_permu(L)==0 alors retourne faux; fsi;
fpour;
pour j de 0 jusque n-1 faire
L:=A[k,irem(j-k,n)]$(k=0..n-1);
si is_permu(L)==0 alors retourne faux; fsi;
fpour;
retourne vrai;
}
:;

15.2.3 Les carrés magiques eulériens pandiagonaux

Écrire un programme Xcas qui teste si une matrice est un carré magique eulérien pandiagonal.
On tape dans un éditeur de programme :

esteulerp(A):={
local n,s,j,k,rep,L,C,D,M;
L:=mat2list(A);
si is_permu(L)==0 alors retourne faux fsi;
rep:=true;
n:=size(A);
s:=n*(n^2-1)/2;
L:=unapply(sum(A[j,k],k=0..n-1),j);
C:=unapply(sum(A[j,k],j=0..n-1),k);
D:=unapply(sum(A[j,irem(j+k,n)],j=0..n-1),k);
M:=unapply(sum(A[j,irem(k-j,n)],j=0..n-1),k);
pour j de 0 jusque n faire 
  si L(j)!=s ou C(j)!=s ou D(j)!=s ou M(j)!=s alors 
    rep:=faux; break;
  fsi;
fpour;
retourne rep;
}
:;

On remarque que si les n lignes et n−1 colonnes (resp n lignes et n−1 diagomales montantes, n lignes et n−1 diagomales descendantes) sont de même somme s alors les n colonnes (resp les n diagomales montantes, les n diagomales descendantes) sont de même somme s. On tape plus simplement pour savoir si A est un carré eulérien pandiagonal :

estpandiage(A):={
local j,k,n,s,L;
L:=mat2list(A);
si is_permu(L)==0 alors retourne faux fsi;
n:=size(A);
s:=n*(n^2-1)/2;
si [sum(A[j,k],j,0,n-1)$(k=0..n-1)]!=[s $(k=0..n-1)] alors 
retourne faux; 
fsi;
si [sum(A[k,j],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
si [sum(A[j,irem(j+k,n)],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
si [sum(A[j,irem(-j+k,n)],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
retourne vrai;
}
:;

15.2.4 La règle de Manuel Moscopule (14ième siécle) ou règle du cavalier

Cette règle permet d’écrire des carrés magiques eulériens pandiagonaux d’ordre n lorsque n est impair et non divisible par 3.
On considère le carré comme un tore et on applique la règle :

Placez 0 dans la case de votre choix (case l,c du programme),
puis, avancez horizontalement de 2 cases et descendez verticalement d’une case et placez le 1 (mouvement du cavalier aux echecs),
faites de même pour les nombres suivants jusqu’au placement de n−1,
reculez horizontalement de 1 case et placez alors le nombre n,
refaites le même processus jusque 2n−1, puis reculez horizontalement de 1 case et placez alors le nombre 2n etc...

Écrire un programme Xcas qui renvoie un carré magique eulérien construit selon cette règle.
On tape dans un éditeur de programme :

cavalier(n,l,c):={
local j,k,A;
si irem(n,2)==0 ou irem(n,3)==0 
  alors retourne "n !=2k et n !=3k"; 
fsi
l:=irem(l,n);c:=irem(c,n);
A:=idn(n);
pour j de 0 jusque n-1 faire
  pour k de 0 jusque n-2 faire
    A[l,c]:=k+n*j;
    l:=irem(l+1,n);
    c:=irem(c+2,n);
  fpour;
A[l,c]:=k+n*j;
c:=irem(c-1,n);
fpour;
return A;
}
:;

On tape : C:=cavalier(5,0,0)
On obtient :
[[0,24,18,12,6],[13,7,1,20,19],[21,15,14,8,2], [9,3,22,16,10],[17,11,5,4,23]] c’est à dire :

0	24	18	12	6
13	7	1	20	19
21	15	14	8	2
9	3	22	16	10
17	11	5	4	23

On peut traduire cela avec des couleurs. On tape :

lignec(n,k,C):={
local j,L;
L:=NULL;
pour j de 0 jusque n-1 faire 
L:=L,affichage(carre(j+i*k,j+1+i*k),C[j]+rempli);
fpour;
return L;
}:;
carrec(n,C):={
local j,L,R;
R:=NULL;
pour j de 0 jusque n-1 faire
L:=lignec(n,n-j,C[j]) 
R:=R,L;
fpour;
return R;
}:;

Puis, carrec(5,C) renvoie :

Remarque
Si on affiche les nombres k modulo n (i.e. irem(k,n)), on obtient un carré magique latin (latin veut dire que chacun des entiers 0..n−1 apparaissent dans chaque horizontale et verticale du carré et magique veut dire que la somme des éléments de chaque ligne, de chaque colonne et des 2 diagonales sont identiques et égales à n(n²−1)/2). Pour l’exemple précédent, on tape :
CR:=irem(cavalier(5,0,0),5) et carrec(5,CR) on obtient :

0	4	3	2	1
3	2	1	0	4
1	0	4	3	2
4	3	2	1	0
2	1	0	4	3

On peut visualiser le déplacement du cavalier en mettant dans chaque case iquo(k,n) ce qui donne encore un carré latin. Pour l’exemple précédent, on tape :
CQ:=(C-CQ)/5) et carrec(5,CQ), on obtient :
Pour l’exemple précédent, on obtient :

0	4	3	2	1
2	1	0	4	3
4	3	2	1	0
1	0	4	3	2
3	2	1	0	4

15.2.5 Produit de 2 carrés magiques

Pour construire des carrés eulériens pandiagonaux, il est souvent plus agéable d’écrire les coefficients du carré d’ordre n en base n. Tout entier compris entre 0 et n²−1 s’écrit de manière unique sous la forme n*a+b où a et b sont des entiers compris entre 0 et n−1.
Définition
On appelle produit AXB de 2 carrés magiques A=a_j,k et B=b_j,k de taille n vérifiant a_j,k ∈ [0..n−1] et b_j,k ∈ [0..n−1], le carré C=c_j,k de taille n tel que :
c_j,k=na_j,k+b_j,k (i.e a_j,k,b_j,k est l’écriture en base n de c_j,k).
Donc, C:=cavalier(5,0,0) se décompose en le produit de 2 carrés latins pandiagonaux :

0	24	18	12	6
13	7	1	20	19
21	15	14	8	2
9	3	22	16	10
17	11	5	4	23

0	4	3	2	1
2	1	0	4	3
4	3	2	1	0
1	0	4	3	2
3	2	1	0	4

0	4	3	2	1
3	2	1	0	4
1	0	4	3	2
4	3	2	1	0
2	1	0	4	3

On peut traduire cela avec des couleurs.
On tape :

lignecc(n,k,C1,C2):={
local j,L;
L:=NULL;
pour j de 0 jusque n-1 faire 
L:=L,affichage(rectangle(j+i*k,j+1/2+i*k,2),C1[j]+rempli),
     affichage(rectangle(j+1/2+i*k,j+1+i*k,2),C2[j]+rempli);
fpour;
return L;
}:;
carrecc(n,C1,C2):={
local j,L,R;
R:=NULL;
pour j de 0 jusque n-1 faire
L:=lignecc(n,n-j,C1[j],C2[j]) 
R:=R,L;
fpour;
return R;
}
:;

Puis, C:=cavalier(5,0,0);CR1:=iquo(C,5);CR2:=irem(C,5) carrecc(5,CR1,CR2) renvoie :

15.2.6 Démonstration de l’algorithme du cavalier

Pour cela on va déterminer une expression générale de A[j,k] en fonction de j et k lorsque l’on met A[0,0]=0 et que l’on applique l’algorithme du cavalier.
Pour cela on écrit A[j,k] en base n :
A[j,k]=na_j,k+b_j,k avec a_j,k∈ [0..n−1] et b_j,k∈ [0..n−1].
On a d’après l’algorithme du cavalier :
a_0,0=0 et b_0,0=0 a_j+1,k+2=a_j,k et b_j+1,k+2=b_j,k+1 si 0≤ b_j,k<n−1 et
a_j,k−1=a_j,k+1 et b_j,k−1=b_j,k+1=0 modn si b_j,k=n−1
Le nombre A[j,k]=na_j,k+b_j,k a donc comme indice de ligne j=b_j,k−a_j,k modn.
En effet, quand a_j,k=0 on a j=b_j,k, puis quand a_j,k=1 et b_j,k=0 on a j=n−1=b_j,k−a_j,k modn etc...
Le nombre A[j,k]=na_j,k+b_j,k a donc comme indice de colonne k=2b_j,k−3a_j,k modn.
En effet, quand a_j,k=0 on a k=2b_j,k modn, donc on a bien k=2b_j,k−3a_j,k modn
puis quand a_j,k=1 et b_j,k=0 on a b_j,k+1=b_j,k−1 modn et a_j,k+1=a_j,k−1 donc :
b_j,k=b_j,k+1+1=0 modn et
k+1=2b_j,k+1−3a_j,k+1=2b_j,k−2−3a_j,k+3=2b_j,k−3a_j,k+1 modn (car a_j,k+1=0 et d’après ce qui précéde si a_j,k+1=0 on a k+1=2b_j,k+1 modn et b_j,k−1+1=0 modn) donc k=2b_j,k−3a_j,k modn etc...
On a donc :
j=b_j,k−a_j,k modn et k=2b_j,k−3a_j,k modn donc
2j−k=a_j,kmodn et 3j−k=b_j,kmodn donc
a_j,k=2j−k modn et b_j,k=3j−k modn.
A est un carré eulérien pandiagonal. En effet, les nombres A[j,k] sont tous différents, car si na_j1,k1+b_j1,k1=na_j2,k2+b_j2,k2 alors
a_j1,k1=a_j2,k2 et b_j1,k1=b_j2,k2 donc
2j1−k1 =2j2−k2 modn et 3j1−k1 =3j2−k2 modn donc
k2−k1=2j2−2j1=3j2−3j1 donc j1=j2 et k1=k2.
Sur les a_j,k et les b_j,k forment un carré latin pandiagonal d’odre n car sur une même ligne les a_j,k (respectivement les b_j,k) sont tous différents en effet : si a_j1,k1=a_j1,k2 (resp b_j1,k1=b_j1,k2) alors
2j1−k1 =2j1−k2 modn et 3j1−k1 =3j1−k2 modn donc k1=k2. Si n n’est pas un multiple de 2 ni un multiple de 3, sur une même colonne les a_j,k (respectivement les b_j,k) sont tous différents en effet : si a_j1,k1=a_j2,k1 (resp b_j1,k1=b_j2,k1) alors
2j1−k1 =2j2−k1 modn (resp 3j1−k1 =3j2−k1 modn)
donc 2(j1−j2)=0 modn (resp 3(j1−j2)=0 modn) comme 2 et ne divisent pas n on en déduit que j1=j2. Sur les diagonales descendantes les a_j,k (respectivement les b_j,k) sont tous différents en effet si :
a_j1,k1+j1=a_j2,k1+j2 (resp b_j1,k1+j1=b_j2,k1+j2) alors
2j1−k1−j1 =2j2−k1−j2 modn et 3j1−k1−j1 =3j2−k1−j2 modn donc j1=j2 (resp j1=j2 car 2 ne divise pas n) Sur les diagonales montantes les a_j,k (respectivement les b_j,k) sont tous différents en effet si :
a_j1,k1−j1=a_j2,k1−j2 (resp b_j1,k1−j1=b_j2,k1−j2) alors
2j1−k1+j1 =2j2−k1+j2 modn et 3j1−k1+j1 =3j2−k1+j2 modn donc j1=j2 car 3 et 4 ne divisent pas n. Donc les carrés a_j,k et b_j,k sont des carrés latins pandiagonaux. Comme les nombres A[j,k] sont tous différents, on en déduit que A est un carré eulérien pandiagonal.

15.2.7 Généralistion de l’algorithme du cavalier pour n≠ 2p et n≠ 3p

Lorsque n=5 l’algorithme du cavalier a produit un carré eulérien pandiagonal qui était le produit de 2 carrés latins pandiagonaux. On va donc essayer de produire des carrés eulériens pandiagonaux comme produit de 2 carrés latins pandiagonaux.
Définition
On dit que p est un générateur interne de ℤ/nℤ si p, p−1 et p+1 sont des générateurs de ℤ/nℤ (i.e p, p−1 et p+1 doivent être premier avec n).
Remarque si n est pair ou si n est un multiple de 3, ℤ/nℤ ne posséde pas de générateur interne.
Revenons à l’exemple obtenu avec la règle du cavalier pour n=5 : C = A X B =

0	24	18	12	6
13	7	1	20	19
21	15	14	8	2
9	3	22	16	10
17	11	5	4	23

0	4	3	2	1
2	1	0	4	3
4	3	2	1	0
1	0	4	3	2
3	2	1	0	4

0	4	3	2	1
3	2	1	0	4
1	0	4	3	2
4	3	2	1	0
2	1	0	4	3

On remarque que :
le carré A est obtenu en mettant sur la première ligne, une permutation σ de 0..4 (ici σ([0,1,2,3,4])=[0,4,3,2,1]), puis la deuxième ligne est obtenue en décalant la première ligne vers la droite de 2 cases (i.e. A[1,k)=A[0,k+2] pour k=0..4) ce qui donne [2,1,0,4,3] etc...
le carré B est obtenu en mettant sur la première ligne la même permutation de 0..4 [0,4,3,2,1], puis la deuxième ligne est obtenue en décalant la première ligne vers la droite de 3 cases (i.e. B[1,k)=A[0,k+3] pour k=0..4) ce qui donne [3,2,1,0,4] etc...
On établit les résultats suivants :
Théorème1 La donnée de toute permutation σ de 0..n−1 et de tout générateur p interne de ℤ/nℤ définit un carré latin de taille n.
Définition le carré latin ainsi construit est dit de type (σ, p).
Si A est un carré latin de taille n et de type (σ, p) on a :
A[0,k)=σ([0,..n−1]) pour k=0..n−1
A[j+1,k)=A[j,k+p modn] pour j=0..n−1 et pour k=0..n−1
p engendre ℤ/nℤ donc p modn, p+1 modn, p+n−1 modn est une permutation de [0,..n−1].
Donc les lignes de A sont des permutations de [0,..n−1]
Les colonnes de A sont telles que :
A[j,0]=A[j−1,p]=A[j−2,2p modn]=..A[0,j*pmodn] et
pour pour j fixé et k=0..n−1, on a :
A[j,k]=A[j−1,p+kmodn]=A[j−2,2p+kmodn]=..=A[0,j*p+kmodn]
Donc les colonnes de A sont des permutations de [0,1..n−1]
Les diagonales descendantes de A sont telles que pour k fixé et j=0..n−1 on a :
A[j,j+kmodn]=A[0,j*(p+1)+kmodn]
p+1 engendre ℤ/nℤ donc les diagonales descendantes de A sont des permutations de [0,..n−1]
Les diagonales montantes de A sont telles que pour k fixé et j=0..n−1 on a :
A[j,−j+kmodn]=A[0,j*(p−1)+kmodn]
p−1 engendre ℤ/nℤ donc les diagonales montantes de A sont des permutations de [0,..n−1].
Théorème2 Le produit de 2 carrés latins de taille n et de types (σ, p) et (σ, q) est un carré eulérien pandiagonal si p−q modn est un générateur de ℤ/nℤ.
En effet, soient A et B deux carrés d’ordre n où A est de type (σ, p) et B est de type (σ, q). (où σ est une bijection de [0,1..n−1] dans [0,1..n−1] et p−1modn, p, p+1modn, q−1modn, q, q−1modn, p−q modn sont des générateurs de ℤ/nℤ).
On a par construction de A et B :
σ(k)=A[0,k]=B[0,k]
A[1,k]=A[0,k−p modn]=σ(k−pmodn) et
A[j,k]=A[j,k−p*j modn]=σ(k−p*jmodn)
B[1,k]=B[0,k−q modn]=σ(k−qmodn) et
B[j,k]=B[j,k−q*j modn]=σ(k−q*jmodn)
On pose C[j,k]=n*A[j,k]+B[j,k] et montrons que C est un carré eulérien pandiagonal.
Chacun des entiers compris entre 0 et n²−1 sont les coefficients de C. En effet les coefficients de C sont dans [0,1..n−1] et ils sont tous différents car si :
C[j1,k1]=n*A[j1,k1]+B[j1,k1]=C[j2,k2]=n*A[j2,k2]+B[j2,k2], on a :
A[j1,k1]=A[j2,k2] et B[j1,k1]=B[j2,k2] (unicité de l’écriture en base n) c’est à dire :
σ(k1−p*j1modn)=σ(k2−p*j2modn) et
σ(k1−q*j1modn)=σ(k2−q*j2modn)= et comme σ est une bijection on a :
k1−k2=p*(j1−j2)=q(j1−j2) modn donc (p−q)(j1−j2)=0modn donc j1=j2 (puisque p−q modn est un générateur de ℤ/nℤ) et k1=k2. Le carré C est pandiagonal car les 4n sommes des lignes, des colonnes, des diagonales de A et de B sont égales à n(n−1)/2 (d’après le th 1) donc les sommes des lignes, des colonnes, des diagonales de C sont égales à (n+1)n(n−1)/2=n(n²−1)/2

15.2.8 Les programmes

Le produit de 2 carrés de ℤ/nℤ

Voici le programme du produit de 2 carrés A=a_j,k et B=b_j,k de taille n vérifiant a_j,k ∈ [0,1..n−1]. On écrit le programme estdansnz(A) qui vérifie que les A[j,k] sont dans 0,1,..n−1 lorsque A est une matrice carrée de dimension n.
Puis, on écrit le programme produitcar(A,B) qui renvoie le produit de 2 carrés de dimension n dont les éléments sont dans 0,1,..n−1.
On tape :

estdansnz(A):={
local L,j,n1,rep;
L:=mat2list(A);
n1:=dim(L)-1;
rep:=vrai;
pour j de 0 jusque n1 faire
si L[j]<0 ou L[j]>n1 alors retourne faux; fsi;
fpour;
retourne vrai;
}:;
produitcar(A,B):={
local j,k,C,sa,sb,n;
n:=size(A);
sa:=dim(A);
sb:=dim(B);
si sa!=[n,n] ou sb!=[n,n] ouestdansnz(A)==faux ou estdansnz(B)==faux alors 
retourne "erreur"; fsi;
C:=idn(n); 
pour j de 0 jusque n-1 faire
pour k de 0 jusque n-1 faire
C[j,k]:=n*A[j,k]+B[j,k];
fpour;
fpour;
retourne C;
}:;

On tape :
A:=[[0,4,3,2,1],[2,1,0,4,3],[4,3,2,1,0],[1,0,4,3,2],[3,2,1,0,4]]
B:=[[0,4,3,2,1],[3,2,1,0,4],[1,0,4,3,2],[4,3,2,1,0],[2,1,0,4,3]]
C:=produitcar(A,B)
On obtient :
[[0,24,18,12,6],[13,7,1,20,19],[21,15,14,8,2],[9,3,22,16,10],[17,11,5,4,23]]
On tape :
estpandiage(C)
On obtient :
vrai

Les permutations de 0..n

Nous allons écrire un algorithme qui va renvoyer toutes les permutations de l=[0..n−1] Les fonctions que l’on va écrire vont utiliser la fonction echange.

//echange ds l les elements d'indices j et k
echange(l,j,k):={
local a;
a:=l[j];
l[j]:=l[k];
l[k]:=a;
return l;
}:;

On peut décrire l’arbre des permutations de la liste l[0..n−1] :
à partir de la racine on a n=size(l) branches. Chaque branche commence respectivement par chacun des éléments de la liste l.
On va donc parcourir cet arbre de la racine (nœud de niveau 0) aux différentes extrémités, en renvoyant la liste des branches parcourues pour arriver à cette extrémité.
On va parcourir cet arbre en parcourant les n branches. On numérote ces n branches par p=0..n−1 et le niveau des nœuds q=0..n−1.
On aura donc n appels récursifs.
Chaque branche p (p=0..n−1) peut être considérée à leur tour comme un arbre ayant n−1 branches. La branche p aboutit aux permutations qui laissent invariant le p-ième élément de l (l[p−1]). C’est cet élément que l’on va échanger avec l[0] pour que chaque branche p laisse invariant l’ élément l[0].
On sait que l’on est arrivé au bout de la branche, quand on se trouve au nœud de niveau n−1, dans ce cas la permutation chechée est l (c’est la permutation obtenue à partir de l en laissant ces n−1 premiers éléments invariants).
On utilise une variable locale lr, égale à la liste à renvoyer et un paramètre k, pour que permuts(l,k) renvoie toutes les permutations de l qui laissent invariant les k premiers éléments de l. On tape :

//permuts([1,2,3,4],0) utilise echange 
permuts(l,k):={
local lr,j;
if (k==size(l)-1) return [l];
lr:=[];
for (j:=k;j<size(l);j++){
l:=echange(l,k,j);
lr:=[op(lr),op(permuts(l,k+1))];
}
return lr;
}:;

Remarque On n’est pas obligé de remettre la suite l à sa valeur de départ pour recommencer l’itération puisque le premier échange dans l’itération revient à transformer l en la liste où on a mis son j-ième élément en tête (j=0..n−1).
Comme il faut 2 paramètres pour écrire la fonction récursive permuts, on écrit la fonction permutation qui utilise permuts:

//l:=[0,1,2,3];permutation(l); 
//renvoie toutes les permutations de l
//utilise permuts
permutation(l):={
return permuts(l,0);
};

On tape :
permutation([0,1,2])
On obtient :
[[0,1,2],[0,2,1],[1,0,2],[1,2,0],[2,0,1],[2,1,0]]

Les générateurs internes de ℤ/nℤ

Définition
On dit que k%n est un générateur interne de ℤ/nℤ si k%n,(k−1)%n,(k+1)%n sont des gérnérateurs de ℤ/nℤ. Donc k%n est un générateur interne de ℤ/nℤ si k,k−1,k+1 sont premiers avec n.
Si n est un multiple de 2 ou 3 il n’y a donc pas de générateurs de ℤ/nℤ.
Si n est premier les générateurs de ℤ/nℤ sont tous les entiers entre 2 et n−2 :2,3..n−2.
Pour faire le programme, on parcourt tous les entiers entre 1 et n−1. On compte combien d’entiers consécutifs sont premiers avec n. Ici c’est j0,..j−1 le j étant celui qui a fait sortir du tantque :
tantque j<=n-1 and d==1 (i.e. j==n ou d=gcd(j,n)!=1)
si ce nombre (qui est égal à j−j0) est supérieur ou égal à 3 on rajoute comme générateur j0+1..j-2.
puis on fait progresser j jusqu’à avoir d=gcd(j,n)==1 ou j==n à la sortie du tantque :
tantque j<=n-1 and d!=1.
Puis on recommence...jusqu’à j==n

latin(P,p):={
local A,j,k;
n:=size(P);
A:=idn(n);
A[0]:=P;
pour j de 1 jusque n-1 faire
pour k de 0 jusque n-1 faire
A[j,k]:=P[irem(k-j*p,n)];
fpour;
fpour;
return A;
}:;
generateur(n):={
local L,d,j,j0;
L:=NULL;
si irem(n,2)==0 or irem(n,3)==0 then return L;fsi;
si isprime(n) alors return j$(j=2..n-2);fsi;
j:=1;
tantque j<=n-1 faire
j0:=j;
d:=gcd(j,n);
tantque j<=n-1 and d==1 faire
j:=j+1;
d:=gcd(j,n);
ftantque;
si j-j0>=3 alors 
L:=L,j$(j=j0+1..j-2);
fsi;
j:=j+1;
d:=gcd(j,n);
tantque j<=n-1 and d!=1 faire
j:=j+1;
d:=gcd(j,n);
ftantque;
ftantque;
return L;
}:;

Fabrication d’un carré eulérien pandiagonal

On tape :

estgenerateur(p,n):={
local G;
p:=irem(p,n);
G:=generateur(n);
si member(p,G)==0 alors return faux;fsi
return vrai;
}:;
carrep(n):={
local G,P,L,j,k,A,B,p,q,s;
si irem(n,3)==0 ou irem(n,2)==0 alors renvoie "erreur2" fsi;
G:=generateur(n);
L:=[j$(j=0..n-1)];
P:=permutation(L);
s:=size(G);
k:=alea(s);
p:=G[k];
k:=alea(s);
q:=G[k];
tantque estgenerateur(p-q,n)==0 faire
k:=alea(s);
q:=G[k];
ftantque;
s:=size(P);
k:=alea(s);
P:=P[k];
A:=latin(P,p);
B:=latin(P,q);
retourne produitcar(A,B);
}
:;

Voici le regroupemenr de tous les programmes utilisés :

estpandiage(A):={
local j,k,n,s,L;
L:=mat2list(A);
si is_permu(L)==0 alors retourne faux fsi;
n:=size(A);
s:=n*(n^2-1)/2;
si [sum(A[j,k],j,0,n-1)$(k=0..n-1)]!=[s $(k=0..n-1)] alors 
retourne faux; 
fsi;
si [sum(A[k,j],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
si [sum(A[j,irem(j+k,n)],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
si [sum(A[j,irem(-j+k,n)],j,0,n-1)$(k=0..n-2)]!=[s $(k=0..n-2)] alors 
retourne faux; 
fsi;
retourne vrai;
}
:;
estdansnz(A):={
local L,j,n1,rep;
L:=mat2list(A);
n1:=dim(L)-1;
rep:=vrai;
pour j de 0 jusque n1 faire
si L[j]<0 ou L[j]>n1 alors retourne faux; fsi;
fpour;
retourne vrai;
}:;
produitcar(A,B):={
local j,k,C,sa,sb,n;
n:=size(A);
sa:=dim(A);
sb:=dim(B);
si sa!=[n,n] ou sb!=[n,n] ou estdansnz(A)==faux ou estdansnz(B)==faux alors 
retourne "erreur1"; fsi;
C:=idn(n); 
pour j de 0 jusque n-1 faire
pour k de 0 jusque n-1 faire
C[j,k]:=n*A[j,k]+B[j,k];
fpour;
fpour;
retourne C;
}:;
echange(l,j,k):={
local a;
a:=l[j];
l[j]:=l[k];
l[k]:=a;
return l;
}:;
permuts(l,k):={
local lr,j;
if (k==size(l)-1) return [l];
lr:=[];
for (j:=k;j<size(l);j++){
l:=echange(l,k,j);
lr:=[op(lr),op(permuts(l,k+1))];
}
return lr;
}:;
permutation(l):={
return permuts(l,0);
}:;
latin(P,p):={
local A,j,k;
n:=size(P);
A:=idn(n);
A[0]:=P;
pour j de 1 jusque n-1 faire
pour k de 0 jusque n-1 faire
A[j,k]:=P[irem(k-j*p,n)];
fpour;
fpour;
return A;
}:;
generateur(n):={
local L,d,j,j0;
L:=NULL;
si irem(n,2)==0 or irem(n,3)==0 then return L;fsi;
si isprime(n) alors return j$(j=2..n-2);fsi;
j:=1;
tantque j<=n-1 faire
j0:=j;
d:=gcd(j,n);
tantque j<=n-1 and d==1 faire
j:=j+1;
d:=gcd(j,n);
ftantque;
si j-j0>=3 alors 
L:=L,j$(j=j0+1..j-2);
fsi;
j:=j+1;
d:=gcd(j,n);
tantque j<=n-1 and d!=1 faire
j:=j+1;
d:=gcd(j,n);
ftantque;
ftantque;
return L;
}:;
estgenerateur(p,n):={
local G;
p:=irem(p,n);
G:=generateur(n);
si member(p,G)==0 alors return faux;fsi
return vrai;
}:;
carrep(n):={
local G,P,L,j,k,A,B,p,q,s;
si irem(n,3)==0 ou irem(n,2)==0 alors renvoie "erreur2" fsi;
G:=generateur(n);
L:=[j$(j=0..n-1)];
P:=permutation(L);
s:=size(G);
k:=alea(s);
p:=G[k];
k:=alea(s);
q:=G[k];
tantque estgenerateur(p-q,n)==0 faire
k:=alea(s);
q:=G[k];
ftantque;
s:=size(P);
k:=alea(s);
P:=P[k];
A:=latin(P,p);
B:=latin(P,q);
retourne produitcar(A,B);
}
:;

On tape :
C:=carrep(7)
On obtient [[16,48,24,8,0,40,32],[26,11,2,41,31,15,42],[1,35,33,18,44,27,10], [34,17,43,21,12,4,37],[46,23,13,3,36,28,19],[7,5,39,30,20,45,22], [38,29,14,47,25,9,6]]
On tape :
estpandiage(C)
On obtient vrai

15.2.9 Les carrés eulériens pandiagonaux d’ordre 2,3 et 4

Y-a-t-il des carres eulériens pandiagonaux d’ordre 2, d’ordre 3, d’ordre 4 ?
Rappel
Dans Xcas il y a l’instruction is_permu qui teste si une liste de dimension n est une permutation de 0..n−1. Dans Xcas il y a l’instruction mat2list qui transforme une matrice en une liste. Ainsi is_permu(mat2list(A)) nous dira si la matrice carrée A de dimension n est un carré eulérien d’ordre n i.e. chacun des nombres 0..n²−1 apparait dans les n² cases du carré. Remarque
Si un carré d’ordre n est eulérien, pour qu’il soit pandiagonal il doit satisfaire à 4n équations. Mais comme la somme :
∑_k=0^n²−1=n²(n²−1)/2, la somme des éléments de chacune des 4n rangées (i.e lignes ou colonnes ou diagonales montantes ou descendantes) vaut donc s=n(n²−1)/2. Il suffit donc de satisfaire à 4n−3 équations (par exemple n équations pour les lignes, n−1 pour les colonnes, n−1 pour les diagonales montantes et n−1 pour les diagonales descendantes).

Cherchons si il y a des carrés magiques pandiagonaux d’ordre 2. Il y a 5 équations à satisfaire pour 4 inconnues.
0n tape :A2:=[[x0,x1],[y0,y1]]; V2:=mat2list(A2)
VS2:=linsolve([x0+x1-3,y0+y1-3,x0+y0-3,x1+y1-3,x0+y1-3,x1+y0-3],V)
On obtient : [3/2,3/2,3/2,3/2]
Les 5 équations ne sont donc pas indépendantes.
Il n’y a donc pas de carrés magiques eulériens pandiagonaux d’ordre 2.
Cela était prévisible car la somme serait égale à 3 et donc on doit mettre 3 dans la ligne qui contient 0 et aussi 3 dans la colonne qui contient 0.

Cherchons si il y a des carrés magiques pandiagonaux d’ordre 3. Il y a 9 équations à satisfaire pour 9 inconnues.
0n tape :A3:=[[x0,x1,x2],[y0,y1,y2],[z0,z1,z2]];V3:=mat2list(A3);
VS3:=linsolve([x0+x1+x2+-12,y0+y1+y2-12,z0+z1+z2-12,x0+y0+z0-12,x1+y1+z1-12,x2+y2+z2-12,x0+y1+z2-12,x1+y2+z0-12,x2+y0+z1-12,x2+y1+z0-12, x0+y2+z1-12,x1+y0+z2-12],V3)
On obtient : [4,4,4,4,4,4,4,4,4]
Il n’y a donc pas de carrés magiques pandiagonaux d’ordre 3.
Cela était encore prévisible car la somme serait égale à 12. On a :
8+3+1=8+4+0=12 donc on ne peut pas mettre des nombres différents, dans la colonne du 8, dans la ligne du 8 et dans les diagonales contenant 8.
Cherchons si il y a des carrés magiques pandiagonaux d’ordre 4. 0n tape :
A4:=[[x0,x1,x2,x3],[y0,y1,y2,y3],[z0,z1,z2,z3],[t0,t1,t2,t3]];
V4:=mat2list(A4)
Il y a 13 équations à satisfaire pour 16 inconnues (s=30). On a donc nos chances !
linsolve([x0+x1+x2+x3-30,y0+y1+y2+y3-30,z0+z1+z2+z3-30, t0+t1+t2+t3-30,x0+y0+z0+t0-30,x1+y1+z1+t1-30,x2+y2+z2+t2-30, x3+y3+z3+t3-30,x0+y1+z2+t3-30,x1+y2+z3+t0-30,x2+y3+z0+t1-30, x3+y0+z1+t2-30,x0+y3+z2+t1-30,x1+y0+z3+t2-30,x2+y1+z0+t3-30, x3+y2+z1+t0-30],V4)
On obtient : [t2+t3+z3-15,-z3+15,-t1-t2+z3+15,t1-t3-z3+15,-t2+15, -t3+15,t1+t2+t3-15,-t1+15,t1+t2-z3,-t1+t3+z3,-t2-t3-z3+30, z3,-t1-t2-t3+30,t1,t2,t3] On en déduit que les 13 équations ne sont pas indépendantes : On remarque que si on fait la sommes des 6 rangées ci-dessous la sommes des cases notées par des points rouges est comptés 3 fois donc ces 4 cases ont aussi comme somme s ce qui entraine que la somme des 4 cases situées aux sommets vaut aussi s.

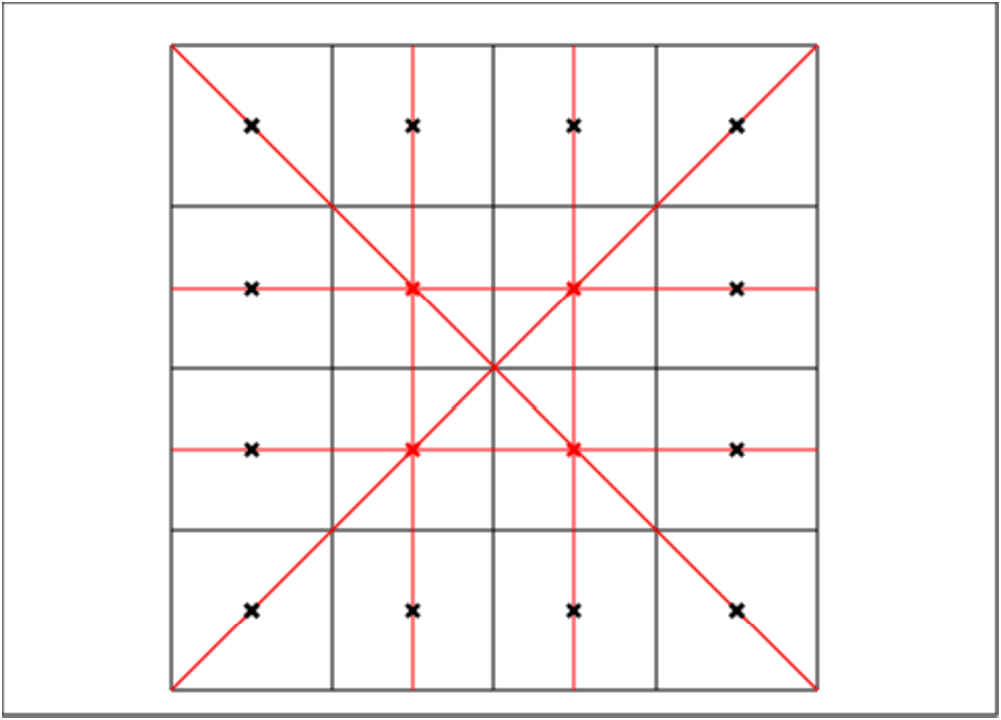
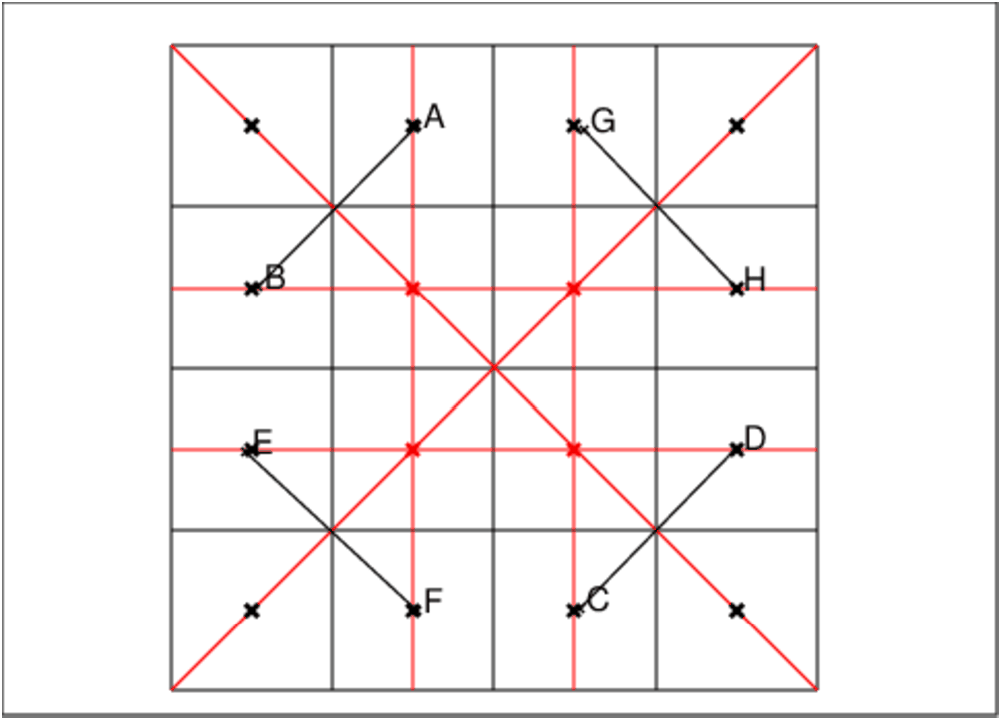
On en déduit que la somme des cases A,B,C,D,E,F,G,H vaut 2s, c’est à dire que si la somme des cases A,B,C,D vaut s cela entraine que la somme des cases E,F,G,H vaut aussi s.
On tape :
L4(z3,t1,t2,t3):=[t2+t3+z3-15,-z3+15,-t1-t2+z3+15,t1-t3-z3+15, -t2+15,-t3+15,t1+t2+t3-15,-t1+15,t1+t2-z3,-t1+t3+z3,-t2-t3-z3+30, z3,-t1-t2-t3+30,t1,t2,t3]
puis on va chercher avec un programme les valeurs de z3,t1,t2,t3 pour lesquelles on a des carrés eulériens. Pour cela on va faire varier les 4 variables z3,t1,t2,t3 entre 0 et 15.
On tape :

carremp4(L):={
local R,z3,t1,t2,t3;
R:=[];
pour z3 de 0 jusque 15 faire
 pour t1 de 0 jusque 15 faire
  pour t2 de 0 jusque 15 faire
   pour t3 de 0 jusque 15 faire
    //si listeab(L(z3,t1,t2,t3),0,15) alors
    si is_permu(L(z3,t1,t2,t3)) alors 
       R:=append(R,[z3,t1,t2,t3]);
    fsi
   fpour;
  fpour;
 fpour;
fpour;
return R;
}:;

On tape :
LS4:=carremp4(L4):;
Après "Evaluation time: 15.58", on obtient "Done"
On tape : size(LS4) et on obtient 384
On tape : list2mat(L4(op(LS4[0])),4)
On obtient [[2,15,8,5],[9,4,3,14],[7,10,13,0],[12,1,6,11]]
Si on échange 2 lignes (ou 2 colonnes) dans un carré pandiagonal, on obtient encore un carré pandiagonal : il y a donc 384/16=24 carrés pandiagonaux vraiement différents. On peut donc améliorer le programme précédent en supposant que t3=15.
On tape :
L41(z3,t1,t2):=L4(z3,t1,t2,15)

carremp41(L):={
local R,z3,t1,t2;
R:=[];
pour z3 de 0 jusque 14 faire
pour t1 de 0 jusque 14 faire
pour t2 de 0 jusque 14 faire
si is_permu(L(z3,t1,t2)) alors R:=append(R,[z3,t1,t2]);fsi;
//si listeab(L(z3,t1,t2),0,15) alors R:=append(R,[z3,t1,t2]);fsi;
fpour;
fpour;
fpour;
return R;
}:;

On tape :
LS41:=carremp41(L41):;
Après "Evaluation time: 1.23" on obtient "Done"
size(LS41) renvoie 24 et
list2mat(L41(op(LS41[0])),4) renvoie
[[5,14,9,2],[11,0,7,12],[6,13,10,1],[8,3,4,15]]
Soit :
C:=[[5,14,9,2],[11,0,7,12],[6,13,10,1],[8,3,4,15]]
On écrit C en base 4 on obtient :
[[11,32,21,2],[23,0,13,30],[12,31,22,1],[20,3,10,33]]

c’est à dire :
C=A X B =

5	14	9	2
11	0	7	12
6	13	10	1
8	3	4	15

1	3	2	0
2	0	1	3
1	3	2	0
2	0	1	3

1	2	1	2
3	0	3	0
2	1	2	1
0	3	0	3

)=
On tape :
A:=[[1,3,2,0],[2,0,1,3],[1,3,2,0],[2,0,1,3]]
B:=[[1,2,1,2],[3,0,3,0],[2,1,2,1],[0,3,0,3]]
C:=produitcar(A,B)
On obtient :
[[5,14,9,2],[11,0,7,12],[6,13,10,1],[8,3,4,15]]
On tape :
estpandiage(C)
On obtient :
vrai
Remarque Pour cet exemple (n=4), dans la décomposition de C en produit AXB les carrés A et B ne sont pas latins.
Cherchons les 24 carrés d’ordre 4 se terminant par 0
On tape :
LL41(z3,t1,t2):=L4(z3,t1,t2,0)
LLS41:=carremp41(L41):;
size(LLS41)
On obtient :
24
On tape :
list2mat(LL41(op(LLS41[1])),4)$(k=0..23)
On obtient :

[[5,8,6,11],[2,15,1,12],[9,4,10,7],[14,3,13,0]],
[[6,8,5,11],[1,15,2,12],[10,4,9,7],[13,3,14,0]],
[[3,8,6,13],[4,15,1,10],[9,2,12,7],[14,5,11,0]],
[[6,8,3,13],[1,15,4,10],[12,2,9,7],[11,5,14,0]],
[[3,8,5,14],[4,15,2,9],[10,1,12,7],[13,6,11,0]],
[[5,8,3,14],[2,15,4,9],[12,1,10,7],[11,6,13,0]],
[[9,4,10,7],[2,15,1,12],[5,8,6,11],[14,3,13,0]],
[[10,4,9,7],[1,15,2,12],[6,8,5,11],[13,3,14,0]],
[[3,4,10,13],[8,15,1,6],[5,2,12,11],[14,9,7,0]],
[[10,4,3,13],[1,15,8,6],[12,2,5,11],[7,9,14,0]],
[[3,4,9,14],[8,15,2,5],[6,1,12,11],[13,10,7,0]],
[[9,4,3,14],[2,15,8,5],[12,1,6,11],[7,10,13,0]],
[[9,2,12,7],[4,15,1,10],[3,8,6,13],[14,5,11,0]],
[[12,2,9,7],[1,15,4,10],[6,8,3,13],[11,5,14,0]],
[[5,2,12,11],[8,15,1,6],[3,4,10,13],[14,9,7,0]],
[[12,2,5,11],[1,15,8,6],[10,4,3,13],[7,9,14,0]],
[[5,2,9,14],[8,15,4,3],[6,1,10,13],[11,12,7,0]],
[[9,2,5,14],[4,15,8,3],[10,1,6,13],[7,12,11,0]],
[[10,1,12,7],[4,15,2,9],[3,8,5,14],[13,6,11,0]],
[[12,1,10,7],[2,15,4,9],[5,8,3,14],[11,6,13,0]],
[[6,1,12,11],[8,15,2,5],[3,4,9,14],[13,10,7,0]],
[[12,1,6,11],[2,15,8,5],[9,4,3,14],[7,10,13,0]],
[[6,1,10,13],[8,15,4,3],[5,2,9,14],[11,12,7,0]],
[[10,1,6,13],[4,15,8,3],[9,2,5,14],[7,12,11,0]]

Dans la gravure Melancolia I d’Albrecht Dürer il y a un carré magique en haut et a droite qui est eulérien (écrit avec les nombres de 1 à 16) mais il n’est pas pandiagonal. Il peut être représenté (avec les nombres de 0 à 15) par :
[[15,2,1,12],[4,9,10,7],[8,5,6,11],[3,14,13,0]]
Ce carré a sur ces lignes les mêmes nombres que sur les lignes de ces 3 carrés pandiagonaux :

[[5,8,6,11],[2,15,1,12],[9,4,10,7],[14,3,13,0]],
[[9,4,10,7],[2,15,1,12],[5,8,6,11],[14,3,13,0]],
[[10,4,9,7],[1,15,2,12],[6,8,5,11],[13,3,14,0]]

15.2.10 Existence de carrés eulériens pandiagonaux d’ordre 6

Y-a-t-il des carres eulériens pandiagonaux d’ordre 6 ? On tape :
V6:=[x0,x1,x2,x3,x4,x5,y0,y1,y2,y3,y4,y5,z0,z1,z2,z3,z4,z5, t0,t1,t2,t3,t4,t5,u0,u1,u2,u3,u4,u5,v0,v1,v2,v3,v4,v5]
M:=list2mat(V6,6)
L(j):=sum(M[j,k],k=0..5)
C(k):=sum(M[j,k],j=0..5)
D(k):=sum(M[j,irem(-j+k,6)],j=0..5)
T(k):=sum(M[j,irem(k+j,6)],j=0..5)
LL:=(L(j)-105)$(j=0..5)
CC:=(C(k)-105)$(k=0..4)
DD:=(D(k)-105)$(k=0..4)
TT:=(T(k)-105)$(k=0..4)
linsolve([LL,CC,DD,TT],V6)[0]
On obtient la valeur de x0 :
t4+t5+u3+u4+u5+v2+v3+v4+v5+z5+(-315)/2
Donc x0 n’est jamais un nombre entier.
Il n’y a donc pas de carrés eulériens pandiagonaux d’ordre 6.

15.3 Les hexagones magiques

15.3.1 Le dessin

Peut-on placer les entiers de 1 à n dans une structure hexagonale ayant n hexagones, de façon à ce que la somme des nombres alignés soit constante ?
Pour une structure hexagonale ayant 7 hexagones:

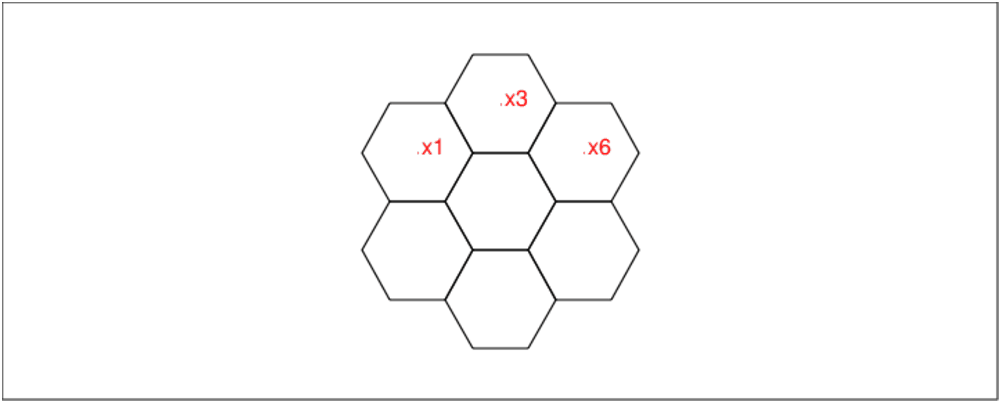
0n voit facilement que cela est impossible puisque si x1+x3=x3+x6 alors x1=x6
Pour une structure hexagonale ayant 19 hexagones, il faut que les nombres 1,2..19 remplissent les 19 cases afin que la somme de toutes les cases alignèes soit égale à 38 (en tout 5*3 équations à satisfaire). Si il y a yne solution, puisque 1+2+...19=190 et qu’il y a en tout 5 rangées disjointes de même somme, la somme de chaque rangèe vaut 190/5=38.

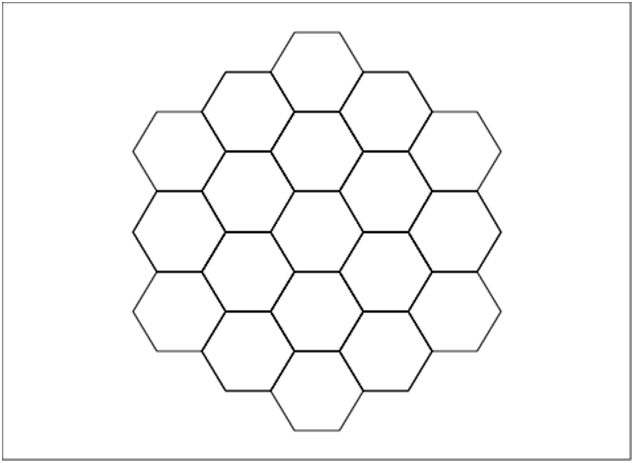
On choisit le nom des variables :

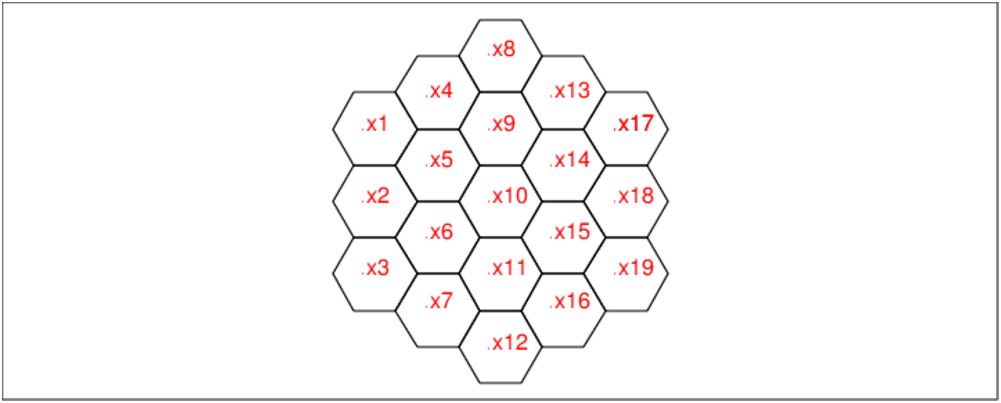
On tape :

linsolve([x1+x2+x3=38,x4+x5+x6+x7=38,x8+x9+x10+x11+x12=38,
x13+x14+x15+x16=38,x17+x18+x19=38,x1+x4+x8=38,x2+x5+x9+x13=38,
x3+x6+x10+x14+x17=38,x7+x11+x15+x18=38,x12+x16+x19=38,
x3+x7+x12=38,x2+x6+x11+x16=38,x1+x5+x10+x15+x19=38,
x4+x9+x14+x18=38,x8+x13+x17=38],
[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,
x11,x12,x13,x14,x15,x16,x17,x18,x19])

On obtient :

[-x10-x11-x14-2*x15-x16-x18-x19+76,x10+x14+x15,
x11+x15+x16+x18+x19-38,x10+x11+x15,x11+x14+x15+x16+x18-38,
-x10-x11-x14-x15-x16+38,-x11-x15-x18+38,x14+x15+x16+x18+x19-38,
-x10-x11-x14-x15-x18+38,x10,x11,-x16-x19+38,
-x14-x15-x16+38,x14,x15,x16,-x18-x19+38,x18,x19]

On voit que les solutions réelles dépendent des 7 variables:
x10,x11,x14,x15,x16,x18,x19.

15.3.2 Le programme

On va donc écrire un programme pour chercher les solutions qui sont des permutations de [1,2,...19].
Pour éviter de faire 19⁷=893871739 itérations on remarque que :
les variables x2 et x4 sont indépendantes de x16,x18,x19 :
les variables x6 et x13 sont indépendantes de x18,x19 :
les variables x5, x7 et x9,x2 et x4 sont indépendantes de x19
On peut remarquer de plus que : x1 (resp x3,x8,x12,x17,x19) ne peut pas être égal à 1 ou à 2 car x1+x2+x3=x1+x4+x8=38 :
si x1=1 cela entraine x2+x3=x4+x8=37. Mais l’équation x+y=37 a comme solution dans 1...19 que les couples (19,18) et (18,19) ce qui ne donne pas 4 solutions distinctes pour x2,x3,x4,x8.
si x1=2 cela entraine x2+x3=x4+x8=36. Mais l’équation x+y=36 a comme solution dans 1...19 les couples (19,17), (18,18) et (17,19) ce qui ne donne pas 4 solutions distinctes pour x2,x3,x4,x8.
On écrit sans trop chercher à optimiser :

hexamagique():={
local x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,
      x13,x14,x15,x16,x17,x18,x19,L,nsol,nsol2;
L:=NULL;
nsol:=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19];
nsol2:=[3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19];
pour x10 de 1 jusque 19 faire
pour x11 de 1 jusque 19 faire
pour x14 de 1 jusque 19 faire
pour x15 de 1 jusque 19 faire
 x2:=x10+x14+x15; x4:=x10+x11+x15;
 si member(x2,nsol) and member(x4,nsol) and x2!=x4 alors
  pour x16 de 1 jusque 19 faire
   x13:=-x14-x15-x16+38;
   x6:=-x10-x11+x13;//x6:=-x10-x11-x14-x15-x16+38
   si member(x13,nsol) and member(x6,nsol) and x13!=x6  alors
    pour x18 de 1 jusque 19 faire
     x7:=-x11-x15-x18+38;
     x5:=-x7+x14+x16;//x5:=x11+x14+x15+x16+x18-38;
     x9:=-x10+x7-x14;//x9:=-x10-x11-x14-x15-x18+38;
     si member(x5,nsol) and member(x7,nsol) and member(x9,nsol) 
        and x5!=x7  and x5!=x9 and x9!=x7 alors
      pour x19 de 3 jusque 19 faire
       x17:=-x18-x19+38; x12:=-x16-x19+38;
       si member(x17,nsol2) and member(x12,nsol2) and 
        x12!=x17 alors
        //x1:=-x10-x11-x14-2*x15-x16-x18-x19+76;
        x1:=-x10-x11-x14-2*x15-x16+x17+38;
        x8:=x14+x15+x16-x17;//x8:=x14+x15+x16+x18+x19-38;
        x3:=x11+x15+x16-x17;//x3:=x11+x15+x16+x18+x19-38;
        si is_permu([x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,
               x13,x14,x15,x16,x17,x18,x19]-[1$19]) alors
         L:=L,[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,
             x13,x14,x15,x16,x17,x18,x19];
        fsi;
       fsi;
      fpour;
     fsi;
    fpour;
   fsi;
  fpour;
 fsi;
fpour;
fpour;
fpour;
fpour;
return L
}:;

On tape :
Rep:=hexamagique()
On obtient (Evaluation time: 1011.94 c’est long ! mais l’employé de chemin de fer, Clifford W. Adams a mis 47 ans de 1910 à 1957 pour trouver une solution avec des hexagones en céramique numérotés de 1 à 19...):

[15,14,9,13,8,6,11,10,4,5,1,18,12,2,7,17,16,19,3],
[16,19,3,12,2,7,17,10,4,5,1,18,13,8,6,11,15,14,9],
[15,13,10,14,8,4,12,9,6,5,2,16,11,1,7,19,18,17,3],
[18,17,3,11,1,7,19,9,6,5,2,16,14,8,4,12,15,13,10],
[3,19,16,17,7,2,12,18,1,5,4,10,11,6,8,13,9,14,15],
[9,14,15,11,6,8,13,18,1,5,4,10,17,7,2,12,3,19,16],
[3,17,18,19,7,1,11,16,2,5,6,9,12,4,8,14,10,13,15],
[10,13,15,12,4,8,14,16,2,5,6,9,19,7,1,11,3,17,18],
[9,11,18,14,6,1,17,15,8,5,7,3,13,4,2,19,10,12,16],
[10,12,16,13,4,2,19,15,8,5,7,3,14,6,1,17,9,11,18],
[16,12,10,19,2,4,13,3,7,5,8,15,17,1,6,14,18,11,9],
[18,11,9,17,1,6,14,3,7,5,8,15,19,2,4,13,16,12,10]

Ces 12 solutions représentent en faite la même solution puisque une solution donne 5 solutions par rotation de k*π/3 pour (k=1..5) et donne 6 solutions par symétrie par rapport aux droites passant par le centre de d’angle k*π/3 pour (k=0..5).
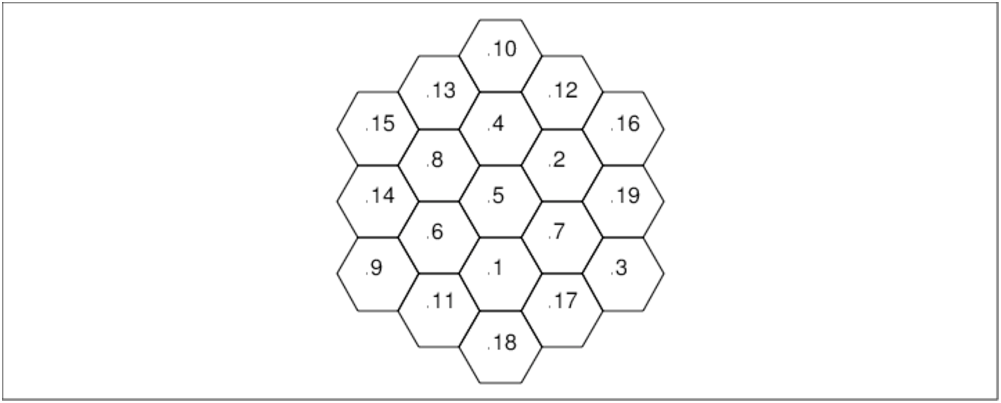
Voici la première solution :

On peut remarquer que l’on peut éliminer les solutions obtenues par rotation en faisant un programme qui impose successivement, par exemple, x11=1, puis x16=1. Mais si x16=1 alors x12+x16+x19=38 entraine x12+x19=37 donc seuls le couples (18,19) et (19,18) sont solutions. Ces 2 solutions donneront des résultas symétriques, donc on va imposer successivement x11=1, puis x16=1, x12=18, x19=19. On aura ainsi les solutions symétriques pour x11=1 mais pas pour x16=1
On va aussi, pour réduire le temps d’exécution, faire un test, à chaque étape, qui vérifie que les valeurs obtenues sont différentes et comprises entre 1 et 19.
Pour cela, on tape tousdiff(L,LR) qui teste si les éléments de L sont tous différents et sont dans la liste LR :

tousdiff(L,LR):={
local s,a;
s:=size(L);
tantque s!=0 faire 
a:=L[0];
si member(a,LR) alors
  L:=remove(a,L);
  si s!=size(L)+1 alors return 0; fsi;
  s:=s-1;
sinon return 0;
fsi
ftantque;
return 1;
}:;

puis on utilise ce test dans hexamagique2() :

hexamagique2():={
local x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,LR,
      x13,x14,x15,x16,x17,x18,x19,L,nsol,nsol2;
LR:=NULL;
nsol:=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19];
x11:=1;
pour x10 de 2 jusque 19 faire
pour x14 de 2 jusque 19 faire
pour x15 de 2 jusque 19 faire
 x2:=x10+x14+x15; x4:=x10+x11+x15;
 L:=[x2,x4,x10,1,x14,x15];
 si tousdiff(L,nsol) alors
  pour x16 de 2 jusque 19 faire
   x13:=-x14-x15-x16+38; x6:=-x10-x11+x13;
   L:=[x2,x4,x6,x10,x11,x13,x14,x15,x16];
   si  tousdiff(L,nsol) alors
    pour x18 de 2 jusque 19 faire
     x7:=-x11-x15-x18+38; x5:=-x7+x14+x16; x9:=-x10+x7-x14;
     L:=[x2,x4,x5,x6,x7,x9,x10,1,x13,x14,x15,x16,x18];
     si  tousdiff(L,nsol) alors
      pour x19 de 3 jusque 19 faire
       x17:=-x18-x19+38; x12:=-x16-x19+38;
       x1:=-x10-x11-x14-2*x15-x16+x17+38;
       x8:=x14+x15+x16-x17; x3:=x11+x15+x16-x17;
       L:=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,1,x12,
              x13,x14,x15,x16,x17,x18,x19];
       si tousdiff(L,nsol) alors
        LR:=LR,L;
       fsi;
      fpour;
     fsi;
    fpour;
   fsi;
  fpour;
 fsi;
fpour;
fpour;
fpour;
x16:=1;x12:=18;x19:=19;
pour x10 de 2 jusque 17 faire
pour x11 de 2 jusque 17 faire
pour x14 de 2 jusque 17 faire
pour x15 de 2 jusque 17 faire
 x2:=x10+x14+x15; x4:=x10+x11+x15;
  x13:=-x14-x15+37;
  x6:=-x10-x11+x13;
  L:=[x2,x4,x6,x10,x11,18,x14,x15,1,x18,19];
  si tousdiff(L,nsol) alors
   pour x18 de 2 jusque 17 faire
    x7:=-x11-x15-x18+38;
    x5:=-x7+x14+x16;
    x9:=-x10+x7-x14;
    x17:=-x18-x19+38;
    x1:=-x10-x11-x14-2*x15-x16+x17+38;
    x8:=x14+x15+x16-x17;
    x3:=x11+x15+x16-x17;
    L:=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,18,
              x13,x14,x15,1,x17,x18,19];
    si  tousdiff(L,nsol) alors
      LR:=LR,L;
    fsi;
   fpour;
  fsi;
fpour;
fpour;
fpour;
fpour;
return LR;
}
:;

On tape :
Rep:=hexamagique2()
On obtient la première solution trouvée tout à l’heure et sa symétrique (Evaluation time: 25.39 on a divisé le temps du premier programme presque par 40 mais on peut certainement faire encore mieux !!!!) :
[15,14,9,13,8,6,11,10,4,5,1,18,12,2,7,17,16,19,3],
[16,19,3,12,2,7,17,10,4,5,1,18,13,8,6,11,15,14,9]

15.3.3 Les programmes des figures

Pour faire le dessin on tape :

hexag2():={
local L,j;
L:=hexagone(-1/2-i*sqrt(3)/2,1/2-i*sqrt(3)/2);
pour j de 0 jusque 5 faire
 L:=L,hexagone((1/2+i*sqrt(3)/2)*exp(i*j*pi/3),exp(i*j*pi/3));
fpour;
L:=L,legende(i*1.73,"x3",red);
L:=L,legende(-1.5+i*0.86,"x1",red);
L:=L,legende(1.5+i*0.86,"x6",red);
retourne L;
}

:;
hexag():={
local L,j;
L:=hexagone(-1/2-i*sqrt(3)/2,1/2-i*sqrt(3)/2);
pour j de 0 jusque 5 faire
 L:=L,hexagone((1/2+i*sqrt(3)/2)*exp(i*j*pi/3),exp(i*j*pi/3)),
hexagone((5/2+i*sqrt(3)/2)*exp(i*j*pi/3),2*exp(i*j*pi/3)),
hexagone((2+i*sqrt(3))*exp(i*j*pi/3),(5/2+i*sqrt(3)/2)*exp(i*j*pi/3));
fpour;
retourne L;
}
:;
hexag2():={
local L,j;
L:=hexagone(-1/2-i*sqrt(3)/2,1/2-i*sqrt(3)/2);
pour j de 0 jusque 5 faire
 L:=L,hexagone((1/2+i*sqrt(3)/2)*exp(i*j*pi/3),exp(i*j*pi/3)),
fpour;
L:=legende(-3.3+i*1.73,"x1",red);
L:=legende(-3.3+i*1.73,"x1",red);
L:=legende(-3.3+i*1.73,"x1",red);
retourne L;
}
:;
leg():={
local L;
L:=legende(-3.3+i*1.73,"x1",red);
L:=L,legende(-3.3,"x2",red);
L:=L,legende(-3.3-i*1.73,"x3",red);
L:=L,legende(-1.8+2.5*i,"x4",red);
L:=L,legende(-1.8+0.86*i,"x5",red);
L:=L,legende(-1.8-0.86*i,"x6",red);
L:=L,legende(-1.8-2.5*i,"x7",red);
L:=L,legende(2.7+i*1.73,"x17",red);
L:=L,legende(2.7,"x18",red);
L:=L,legende(2.7-i*1.73,"x19",red);
L:=L,legende(-0.3+i*3.5,"x8",red);
L:=L,legende(-0.3+i*1.73,"x9",red);
L:=L,legende(-0.3,"x10",red);
L:=L,legende(-0.3-i*1.73,"x11",red);
L:=L,legende(-0.3-i*3.5,"x12",red);
L:=L,legende(1.2+2.5*i,"x13",red);
L:=L,legende(1.2+0.86*i,"x14",red);
L:=L,legende(1.2-0.86*i,"x15",red);
L:=L,legende(1.2-2.5*i,"x16",red);
L;}
:;
valleg(Rep):={
local L,x1;
[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,
 x15,x16,x17,x18,x19]:=Rep[0];
L:=legende(-3.3+i*1.73,string(x1));
L:=L,legende(-3.3,string(x2));
L:=L,legende(-3.3-i*1.73,string(x3));
L:=L,legende(-1.8+2.5*i,string(x4));
L:=L,legende(-1.8+0.86*i,string(x5));
L:=L,legende(-1.8-0.86*i,string(x6));
L:=L,legende(-1.8-2.5*i,string(x7));
L:=L,legende(2.7+i*1.73,string(x17));
L:=L,legende(2.7,string(x18));
L:=L,legende(2.7-i*1.73,string(x19));
L:=L,legende(-0.3+i*3.5,string(x8));
L:=L,legende(-0.3+i*1.73,string(x9));
L:=L,legende(-0.3,string(x10));
L:=L,legende(-0.3-i*1.73,string(x11));
L:=L,legende(-0.3-i*3.5,string(x12));
L:=L,legende(1.2+2.5*i,string(x13));
L:=L,legende(1.2+0.86*i,string(x14));
L:=L,legende(1.2-0.86*i,string(x15));
L:=L,legende(1.2-2.5*i,string(x16));
L;}:;