



suivant: Numerical computations
monter: Animated graphs (2D, 3D
précédent: Animation of a 3D
Table des matières
Index
Animation of a sequence of graphic objects : animation
animation animates the representation of a
sequence of graphic objects
with a given display time. The sequence of objects depends most of
the time of a parameter and is defined using the seq command
but it is not mandatory.
animation takes as argument the sequence of graphic objects.
To define a sequence of graphic objects with seq,
enter the definition of the graphic object (depending on
the parameter), the parameter name, it's minimum value, it's
maximum value maximum and optionnaly a step value.
Input :
animation(seq(plotfunc(cos(a*x),x),a,0,10))
Output :
The sequence of the curves defined by
y = cos(ax), for
a = 0, 1, 2..10
Input :
animation(seq(plotfunc(cos(a*x),x),a,0,10,0.5))
or
animation(seq(plotfunc(cos(a*x),x),a=0..10,0.5))
Output :
The sequence of the curves defined by
y = cos(ax), for
a = 0, 0.5, 1, 1.5..10
Input :
animation(seq(plotfunc([cos(a*x),sin(a*x)],x=0..2*pi/a), a,1,10))
Output :
The sequence of two curves defined by
y = cos(ax) and
y = sin(ax), for a = 1..10 and for
x = 0..2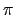 /a
/a
Input :
animation(seq(plotparam([cos(a*t),sin(a*t)], t=0..2*pi),a,1,10))
Output :
The sequence of the parametric curves defined by
x = cos(at) and
y = sin(at), for a = 1..10 and for t = 0..2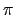
Input :
animation(seq(plotparam([sin(t),sin(a*t)], t,0,2*pi,tstep=0.01),a,1,10))
Output :
The sequence of the parametric curves defined by
x = sin(t), y = sin(at), for a = 0..10 and t = 0..2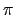
Input :
animation(seq(plotpolar(1-a*0.01*t^2, t,0,5*pi,tstep=0.01),a,1,10))
Output :
The sequence of the polar curves defined by
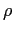 = 1 - a*0.01*t2, for a = 0..10 and t = 0..5
= 1 - a*0.01*t2, for a = 0..10 and t = 0..5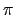
Input :
plotfield(sin(x*y),[x,y]); animation(seq(plotode(sin(x*y),[x,y],[0,a]),a,-4,4,0.5))
Output :
The tangent field of y'=sin(xy) and the sequence of the integral curves crossing through the point (0, a) for a=-4,-3.5...3.5,4
Input :
animation(seq(display(square(0,1+i*a),filled),a,-5,5))
Output :
The sequence of the squares defined by the points 0 and 1+i*a for a = - 5..5
Input :
animation(seq(droite([0,0,0],[1,1,a]),a,-5,5))
Output :
The sequence of the lines defined by the points [0,0,0] and [1,1,a] for a = - 5..5
Input :
animation(seq(plotfunc(x^2-y^a,[x,y]),a=1..3))
Output :
The sequence of the "3D" surface defined by x2 - ya, for a = 1..3 with rainbow colors
Input :
animation(seq(plotfunc((x+i*y)^a,[x,y], display=filled),a=1..10)
Output :
The sequence of the "4D" surfaces defined by (x + i*y)a, for a = 0..10 with rainbow colors
Remark
We may also define the sequence with a program,
for example if we want to draw the
segments of length
1,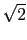 ...
...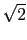 0 constructed with a
right triangle of side 1 and the previous segment
(note that there is a c:=evalf(..) statement
to force approx. evaluation otherwise the computing time
would be too long) :
0 constructed with a
right triangle of side 1 and the previous segment
(note that there is a c:=evalf(..) statement
to force approx. evaluation otherwise the computing time
would be too long) :
seg(n):={
local a,b,c,j,aa,bb,L;
a:=1;
b:=1;
L:=[point(1)];
for(j:=1;j<=n;j++){
L:=append(L,point(a+i*b));
c:=evalf(sqrt(a^2+b^2));
aa:=a;
bb:=b;
a:=aa-bb/c;
b:=bb+aa/c;
}
L;
}
Then input :
animation(seg(20))
We see, each point, one to one with a display time that
depends of the animate value in cfg.
Or :
L:=seg(20); s:=segment(0,L[k])$(k=0..20)
We see 21 segments.
Then, input :
animation(s)
We see, each segment, one to one with a display time that
depends of the animate value in cfg.




suivant: Numerical computations
monter: Animated graphs (2D, 3D
précédent: Animation of a 3D
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![]() ...
...![]() 0 constructed with a
right triangle of side 1 and the previous segment
(note that there is a c:=evalf(..) statement
to force approx. evaluation otherwise the computing time
would be too long) :
0 constructed with a
right triangle of side 1 and the previous segment
(note that there is a c:=evalf(..) statement
to force approx. evaluation otherwise the computing time
would be too long) :