



suivant: 3D parametric surface :
monter: Parametric curves and surfaces
précédent: Parametric curves and surfaces
Table des matières
Index
plotparam([f(t),g(t)],t)
or plotparam(f(t)+i*g(t),t) (resp
plotparam(f(t)+i*g(t),t=t1..t2))
draws the parametric representation of the curve
defined by
x = f (t), y = g(t)
with the default range of values of t (resp for
t1 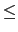 t
t 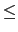 t2).
t2).
The default range of values is taken as specified
in the graphic configuration (t- and t+,
cf. ![[*]](crossref.png) ).
plotparam accepts an optional argument to specify the discretisation
step for t with tstep=.
).
plotparam accepts an optional argument to specify the discretisation
step for t with tstep=.
Input :
plotparam(cos(x)+i*sin(x),x)
or :
plotparam([cos(x),sin(x)],x)
Output :
The unit circle
If in the graphic configuration t goes from -4 to 1, input :
plotparam(sin(t)+i*cos(t))
or :
plotparam(sin(t)+i*cos(t),t=-4..1)
or :
plotparam(sin(x)+i*cos(x),x=-4..1)
Output :
the arc (sin(-4)+i*cos(-4),sin(1)+i*cos(1)) of the unit circle
If in the graphic configuration t goes from -4 to 1, input :
plotparam(sin(t)+i*cos(t),t,tstep=0.5)
Or :
plotparam(sin(t)+i*cos(t),t=-4..1,tstep=0.5)
Output :
A polygon approching the arc (sin(-4)+i*cos(-4),sin(1)+i*cos(1)) of the unit circle




suivant: 3D parametric surface :
monter: Parametric curves and surfaces
précédent: Parametric curves and surfaces
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![[*]](crossref.png) ).
plotparam accepts an optional argument to specify the discretisation
step for t with tstep=.
).
plotparam accepts an optional argument to specify the discretisation
step for t with tstep=.