



suivant: Potential : potential
monter: Multivariate calculus
précédent: Divergence : divergence
Table des matières
Index
Rotationnal : curl
curl takes two arguments : a 3-d vector field
depending on 3 variables.
curl returns the rotationnal of the vector, defined by:
curl([A,B,C],[x,y,z])=
[
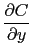
-
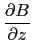
,
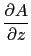
-
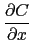
,
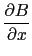
-
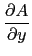
]
Note that n must be equal to 3.
Input :
curl([x*z,-y^2,2*x^y],[x,y,z])
Output :
[2*x^y*log(x),x-2*y*x^(y-1),0]
giac documentation written by Renée De Graeve and Bernard Parisse