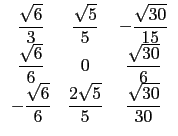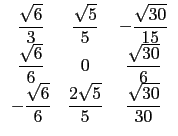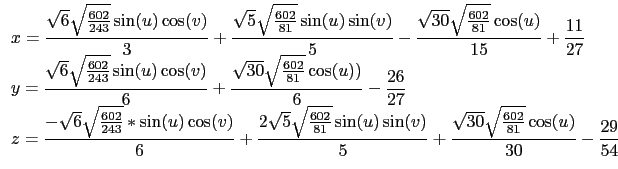



suivant: Multivariate calculus
monter: Quadratic forms
précédent: Graph of a quadric
Table des matières
Index
Quadric reduction : quadrique_reduite
quadrique_reduite takes two arguments : the equation of a
quadric and a vector of variable names.
quadrique_reduite returns a list whose elements are:
- the origin,
- the matrix of a basis where the quadric is reduced,
- 0 or 1 (0 if the quadric is degenerated),
- the reduced equation of the quadric
- a vector with its parametric equations.
Warning !
u,v will be used as parameters of the parametric equations :
these variables should not be assigned (purge them before
calling quadrique_reduite).
Input :
quadrique_reduite(7*x^2+4*y^2+4*z^2+ 4*x*y-4*x*z-2*y*z-4*x+5*y+4*z-18)
Output is a list containing :
- The origin (center of symmetry) of the quadric
[11/27,(-26)/27,(-29)/54],
- The matrix of the basis change:
[[(sqrt(6))/3,(sqrt(5))/5,(-(sqrt(30)))/15],
[(sqrt(6))/6,0,(sqrt(30))/6],
[(-(sqrt(6)))/6,(2*sqrt(5))/5,(sqrt(30))/30]],
- 1 hence the quadric is not degenerated
- the reduced equation of the quadric :
0,9*x^2+3*y^2+3*z^2+(-602)/27,
- The parametric equations (in the original frame) are :
[[(sqrt(6)*sqrt(602/243)*sin(u)*cos(v))/3+
(sqrt(5)*sqrt(602/81)*sin(u)*sin(v))/5+
((-(sqrt(30)))*sqrt(602/81)*cos(u))/15+11/27,
(sqrt(6)*sqrt(602/243)*sin(u)*cos(v))/6+
(sqrt(30)*sqrt(602/81)*cos(u))/6+(-26)/27,
((-(sqrt(6)))*sqrt(602/243)*sin(u)*cos(v))/6+
(2*sqrt(5)*sqrt(602/81)*sin(u)*sin(v))/5+
(sqrt(30)*sqrt(602/81)*cos(u))/30+(-29)/54],
u=(0 .. pi),v=(0.. (2*pi)),ustep=(pi/20),
vstep=((2*pi)/20)]]
Hence the quadric is an ellipsoid and its reduced equation is :
9*x2 +3*y2 +3*z2 + (- 602)/27
after the change of origin
[11/27,(- 26)/27,(- 29)/54],
the matrix of basis change P is :
Its parametric equation is :
Remark :
Note that if the quadric is degenerated and made of 1 or 2 plan(s),
each plan is not given by
its parametric equation but by the list of a point of the plan
and of a normal vector to the plan.
Input :
quadrique_reduite(x^2-y^2+3*x+y+2)
Output :
[[(-3)/2,1/2,0],[[1,0,0],[0,1,0],[0,0,-1]],0,x^2-y^2, [hyperplan([1,1,0],[(-3)/2,1/2,0]), hyperplan([1,-1,0],[(-3)/2,1/2,0])]]




suivant: Multivariate calculus
monter: Quadratic forms
précédent: Graph of a quadric
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse