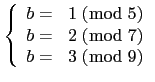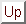



suivant: Chinese remainders for lists
monter: Integers (and Gaussian Integers)
précédent: Solving au+bv=c in :
Table des matières
Index
Chinese remainders : ichinrem, ichrem
ichinrem([a,p],[b,q]) or ichrem([a,p],[b,q]) returns a
list [c,lcm(p,q)] of 2 integers.
The first number c is such that
has the properties
d = a(mod p), d = b(mod q)
If p and q are coprime, a solution d always exists
and all the solutions are congruent modulo p*q.
Examples :
Solve :
Input :
ichinrem([3,5],[9,13])
or input :
ichrem([3,5],[9,13])
Output :
[-17,65]
so x=-17 (mod 65)
we can also input :
ichrem(3%5,9%13)
Output :
-17%65
Solve :
First input :
tmp:=ichinrem([3,5],[4,7])
or input :
tmp:=ichrem([3,5],[4,7])
output :
[-17,35]
then input :
ichinrem([1,9],tmp)
or input :
ichrem([1,9],tmp)
Output :
[-17,315]
hence x=-17 (mod 315)
Alternative :
ichinrem([3%5,4%7,1%9])
Output :
-17%315
Remark
ichrem (orichinrem)may be used to find coefficients of polynomial
which class are known modulo several integers, for example find
ax + b modulo
315 = 5×7×9 under the assumptions:
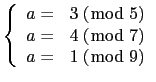
,
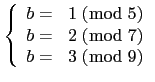
Input :
ichrem((3x+1)%5,(4x+2)%7,(x+3)%9)
Output :
(-17%315× x+156%315
hence a=-17 (mod 315) and b=156 (mod 315).




suivant: Chinese remainders for lists
monter: Integers (and Gaussian Integers)
précédent: Solving au+bv=c in :
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
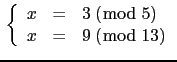
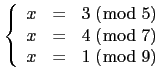
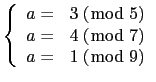 ,
,