Characteristic polynomial using Hessenberg algorithm :
pcar_hessenberg

pcar_hessenberg takes as argument a square matrix A of size n and optionnaly the name of a symbolic variable.
pcar_hessenberg returns the characteristic polynomial P of A written as the list of its coefficients if no variable was provided or written in its symbolic form with respect to the variable name given as second argument, where

P(x) = det(xI - A)

The characteristic polynomial is computed using the Hessenberg algorithm (see e.g. Cohen) which is more efficient (O(n³) deterministic) if the coefficients of A are in a finite field or use a finite representation like approximate numeric coefficients. Note however that this algorithm behaves badly if the coefficients are e.g. in 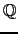$\mathbb {Q}$.
Input :

pcar_hessenberg([[4,1,-2],[1,2,-1],[2,1,0]] % 37)

Output :

[1 % 37 ,-6% 37,12 % 37,-8 % 37]

Input :

pcar_hessenberg([[4,1,-2],[1,2,-1],[2,1,0]] % 37,x)

Output :

x^3-6 %37 *x^2+12 % 37 *x-8 % 37

Hence, the characteristic polynomial of [[4,1,-2],[1,2,-1],[2,1,0]] in $\mathbb {Z}$/37$\mathbb {Z}$ is

x³ -6x² + 12x - 8