



suivant: GCD : Gcd
monter: Integers (and Gaussian Integers)
précédent: The factorial : factorial
Table des matières
Index
GCD : gcd igcd
gcd or igcd denotes the gcd (greatest common divisor)
of several integers (for polynomials see also 1.25.7).
gcd or igcd returns the GCD of all integers.
Input :
gcd(18,15)
Output :
3
Input :
gcd(18,15,21,36)
Output :
3
Input :
gcd([18,15,21,36])
Output :
3
We can also put as parameters two lists of same size (or a matrix with 2
lines), in this case gcd returns the greatest common divisor of
the elements with same index (or of the same column).
Input :
gcd([6,10,12],[21,5,8])
or :
gcd([[6,10,12],[21,5,8]])
Output :
[3,5,4]
An example
Find the greatest common divisor of 4n + 1 and 5n + 3 when
n 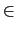
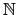 .
.
Input :
f(n):=gcd(4*n+1,5*n+3)
Then, input :
essai(n):={
local j,a,L;
L:=NULL;
for (j:=-n;j<n;j++) {
a:=f(j);
if (a!=1) {
L:=L,[j,a];
}
}
return L;
}
Then, input :
essai(20)
Output :
[-16,7],[-9,7],[-2,7],[5,7],[12,7],[19,7]
So we have now to prove that :
if n! = 5 + k*7 (for
k 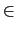
 ), 4n + 1 and 5n + 3 are mutually prime,
), 4n + 1 and 5n + 3 are mutually prime,
and
if n = 5 + k*7 (for
k 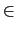
 ), the greatest common divisor of 4n + 1
and 5n + 3 is 7.
), the greatest common divisor of 4n + 1
and 5n + 3 is 7.




suivant: GCD : Gcd
monter: Integers (and Gaussian Integers)
précédent: The factorial : factorial
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse