Lagrange's polynomial : lagrange interp

lagrange takes as argument two lists of size n (resp a matrix with two rows and n columns) and the name of a variable var (by default x).
The first list (resp row) corresponds to the abscissa values x_k (k = 1..n), and the second list (resp row) corresponds to ordinate values y_k (k = 1..n).
lagrange returns a polynomial expression P with respect to var of degree n-1, such that P(x_i) = y_i.
Input :

lagrange([[1,3],[0,1]])

or :

lagrange([1,3],[0,1])

Output :

(x-1)/2

since 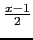${\frac{{x-1}}{{2}}}$ = 0 for x = 1, and 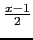${\frac{{x-1}}{{2}}}$ = 1 for x = 3.
Input :

lagrange([1,3],[0,1],y)

Output :

(y-1)/2

Warning
f:=lagrange([1,2],[3,4],y) does not return a function but an expression with respect to y. To define f as a function, input

f:=unapply(lagrange([1,2],[3,4],x),x)

Avoid f(x):=lagrange([1,2],[3,4],x) since the Lagrange polynomial would be computed each time f is called (indeed in a function definition, the second member of the affectation is not evaluated). Note also that
g(x):=lagrange([1,2],[3,4]) would not work since the default argument of lagrange would be global, hence not the same as the local variable used for the definition of g.